http://poj.org/problem?id=1189

Description

有一个三角形木板,竖直立放。上面钉着n(n+1)/2颗钉子，还有(n+1)个格子（当n=5时如图1）。每颗钉子和周围的钉子的距离都等于d，每一个格子的宽度也都等于d，且除了最左端和最右端的格子外每一个格子都正对着最以下一排钉子的间隙。 
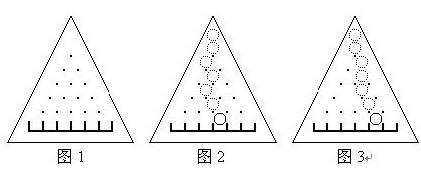
让一个直径略小于d的小球中心正对着最上面的钉子在板上自由滚落，小球每碰到一个钉子都可能落向左边或右边（概率各1/2）。且球的中心还会正对着下一颗将要碰上的钉子。比如图2就是小球一条可能的路径。 
我们知道小球落在第i个格子中的概率pi=pi=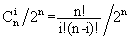，当中i为格子的编号，从左至右依次为0,1,...,n。 
如今的问题是计算拔掉某些钉子后，小球落在编号为m的格子中的概率pm。

假定最以下一排钉子不会被拔掉。比如图3是某些钉子被拔掉后小球一条可能的路径。 

Input

Output

Sample Input

5 2
** .* * ** . * *
* * * * *

Sample Output

7/16

对于每个没有挖掉的钉子(i,j)：dp[i+1][j]+=dp[i][j]/2; dp[i+1][j+1]+=dp[i][j]/2; 对于挖掉的钉子(i,j)：dp[i+2][j+1]+=dp[i][j]; */ #include <stdio.h> #include <string.h> #include <algorithm> #include <iostream> using namespace std; typedef long long LL; bool a[2555]; int n,m; LL dp[55][55]; LL gcd(LL x,LL y) { if(y==0)return x; return gcd(y,x%y); } int main() { while(~scanf("%d%d",&n,&m)) { int k=1; for(int i=1; i<=n; i++) { for(int j=1; j<=i; j++) { char str[12]; scanf("%s",str); if(str[0]=='*') { a[k++]=true; } else { a[k++]=false; } //printf("%d\n",a[k-1]); } //puts(""); } memset(dp,0,sizeof(dp)); dp[1][1]=1LL<<n; for(int i=1; i<=n; i++) { int x=i*(i-1)/2; for(int j=1; j<=i; j++) { if(a[j+x]) { dp[i+1][j]+=dp[i][j]/2; dp[i+1][j+1]+=dp[i][j]/2; } else { dp[i+2][j+1]+=dp[i][j]; } } } LL x=1LL<<n; LL y=dp[n+1][m+1]; LL g=gcd(x,y); printf("%lld/%lld\n",y/g,x/g); } return 0; }