💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
“在SAR系统中,多个独立的视可以由飞行载体以不同的方位角通过观察点时天。
一视由天线沿方位向第一个前向四分之一波束部分产生,下一视则来自下一个四分之一波束,
以此类推。然后,由于来自波束各部分的信号到达雷达接收机是重叠在一起的,所
以在时域或者空域上无法对数据进行分离。然而,具有高方位时间带宽积的一个实用SAR系
统是将时间和频率两者绑定在一起的,在多普勒域内包含了各视的所有信息。也就是说,具
有较高多普勒频率的数据一定是由方位向波束前缘触及到的地形点产生的,而当同一地点出
在方位波束后缘四分之一时,产生了多普勒频段低四分之一部分。”[1]
非相干多视处理(Coherent Sum and Average, CSA)是一种用于雷达通信的信号处理技术。在雷达通信中,使用多个接收机来接收从目标反射回来的信号。CSA技术将多个接收到的信号进行处理,以提高信号的质量和可靠性。
CSA技术的基本思想是利用信号的非相干性质来降低噪声的影响。当多个接收机接收到相同的信号时,由于噪声是随机的,它们在接收到信号时的相位和幅度会有所不同。通过将多个接收到的信号进行相加与平均,可以抵消掉噪声的影响,从而提高信号的信噪比。
CSA技术的具体实现包括以下步骤:
1. 将多个接收机接收到的信号进行对齐,即校准它们的时间延迟和相位差。
2. 将对齐后的信号进行相加,以增强信号的幅度。
3. 将相加后的信号进行平均,以降低噪声的影响。
通过采用CSA技术,可以显著提高雷达通信系统的性能和可靠性。它可以用于各种雷达通信应用,如雷达测距、雷达成像和雷达通信等。
需要注意的是,CSA技术虽然可以提高信号的质量,但也会增加系统的计算复杂性和延时。因此,在实际应用中需要权衡计算资源和性能要求。
📚2 运行结果
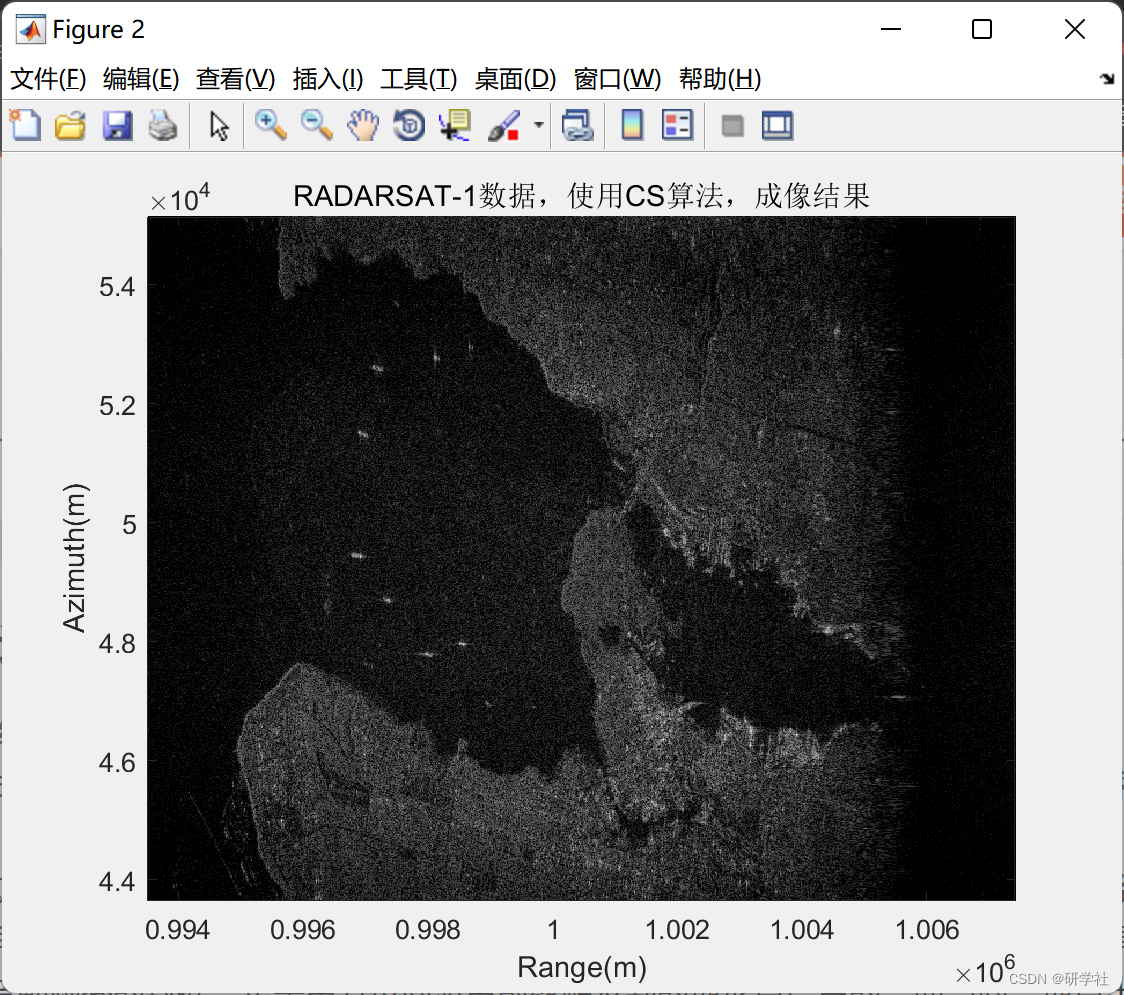
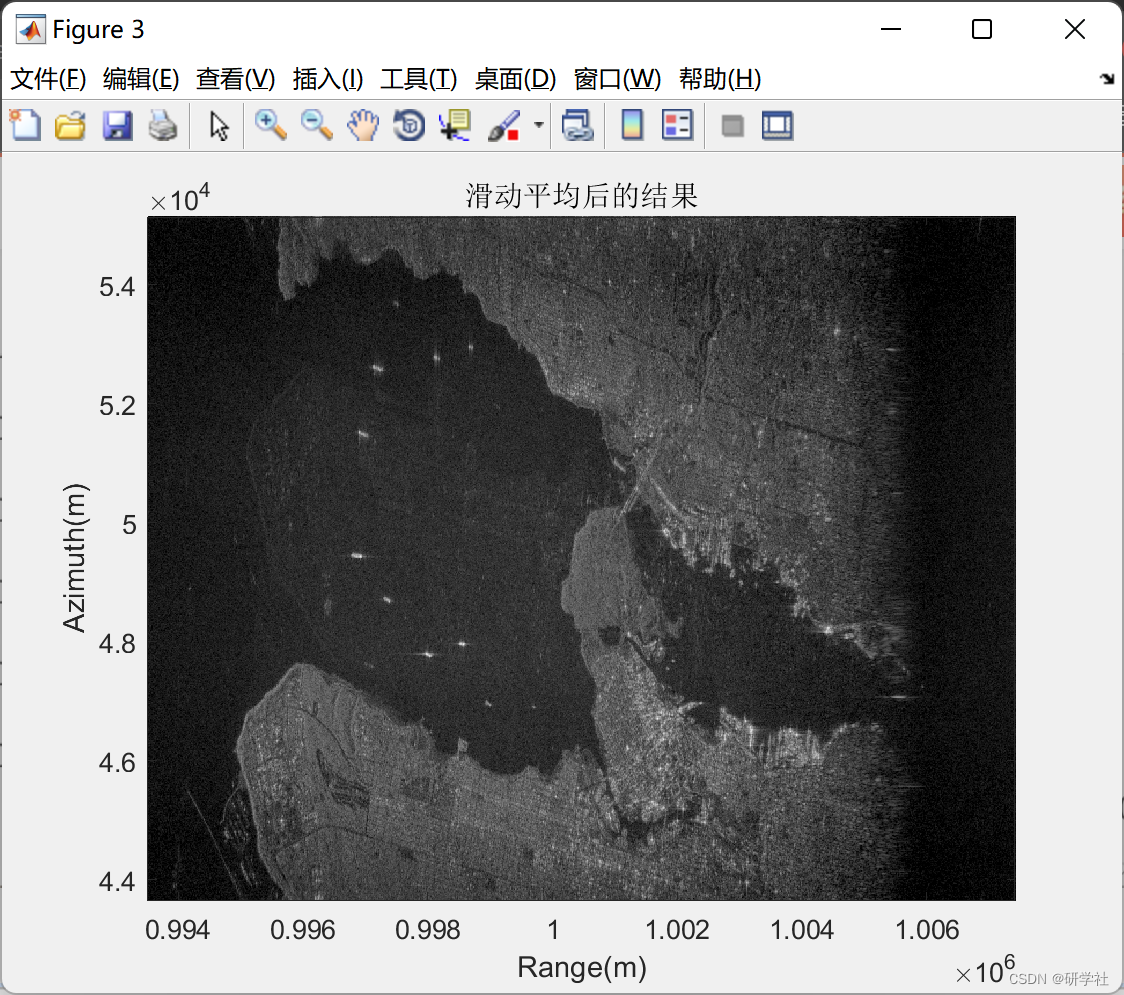
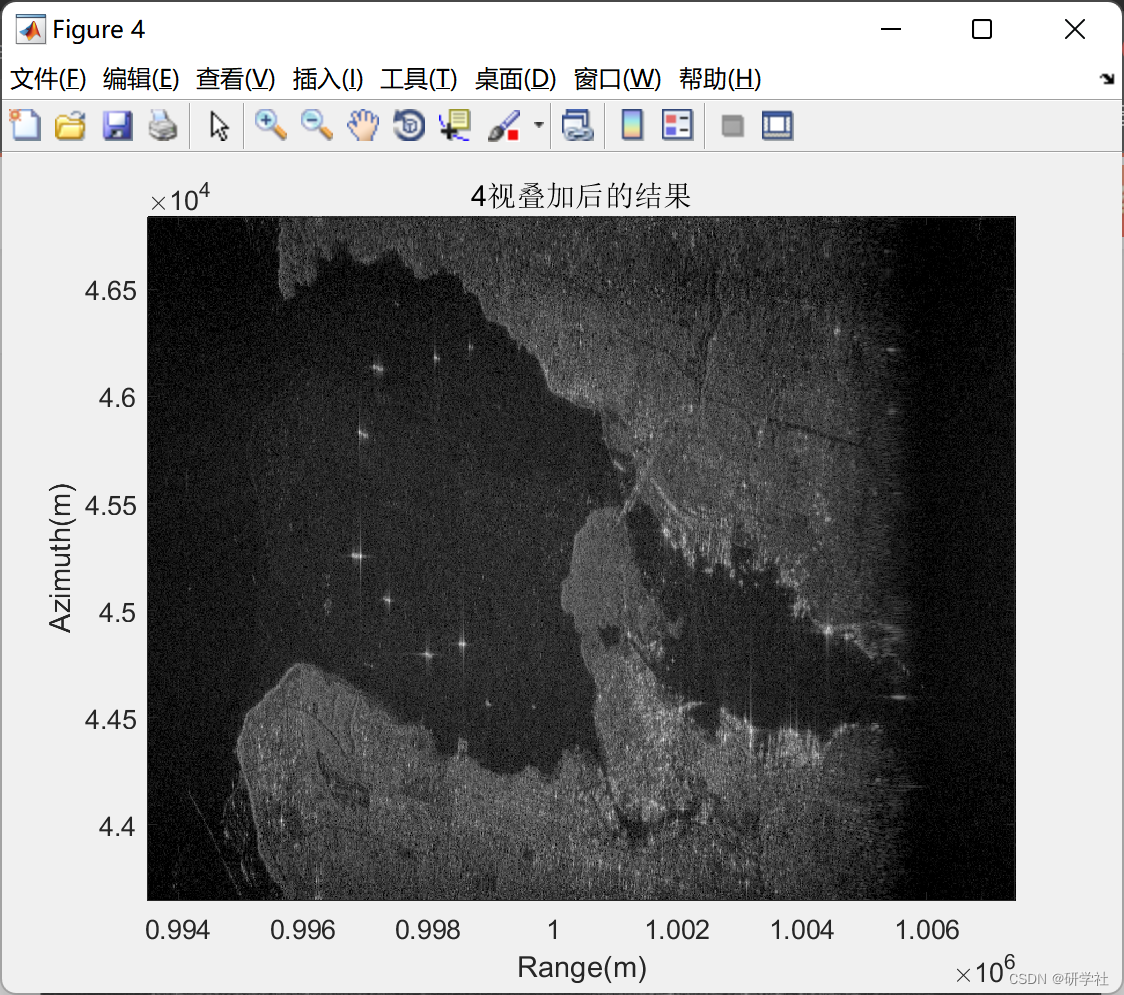
部分代码:
Kr = -Kr; % 将调频率Kr改成负值
BW_range = 30.111e+06; % 脉冲宽度
Vr = 7062; % 有效雷达速率
Ka = 1733; % 方位调频率
fnc = -6900; % 多普勒中心频率
Fa = PRF; % 方位向采样率
lamda = c/f0; % 波长
T_start = 6.5959e-03; % 数据窗开始时间
Nr = round(Tr*Fr); % 线性调频信号采样点数
Nrg = Nrg_cells; % 距离线采样点数
if b == 1 || b == 2
Naz = Nrg_lines_blk; % 每一个数据块的距离线数
else
Naz = Nrg_lines; % 两个数据块,总共的距离线数
end
NFFT_r = Nrg; % 距离向FFT长度
NFFT_a = Naz; % 方位向FFT长度
R_ref = R0; % 参考目标选在场景中心,其最近斜距为 R_ref
fn_ref = fnc; % 参考目标的多普勒中心频率
%%
%
% --------------------------------------------------------------------
% 对原始数据进行补零
% --------------------------------------------------------------------
if b == 1 || b == 2
data = zeros(1*2048,3000);
else
data = zeros(2*2048,3000);
end
data(1:Naz,1:Nrg) = s_echo;
clear s_echo;
s_echo = data;
clear data;
[Naz,Nrg] = size(s_echo);
NFFT_r = Nrg; % 距离向FFT长度
NFFT_a = Naz; % 方位向FFT长度
% 作图显示
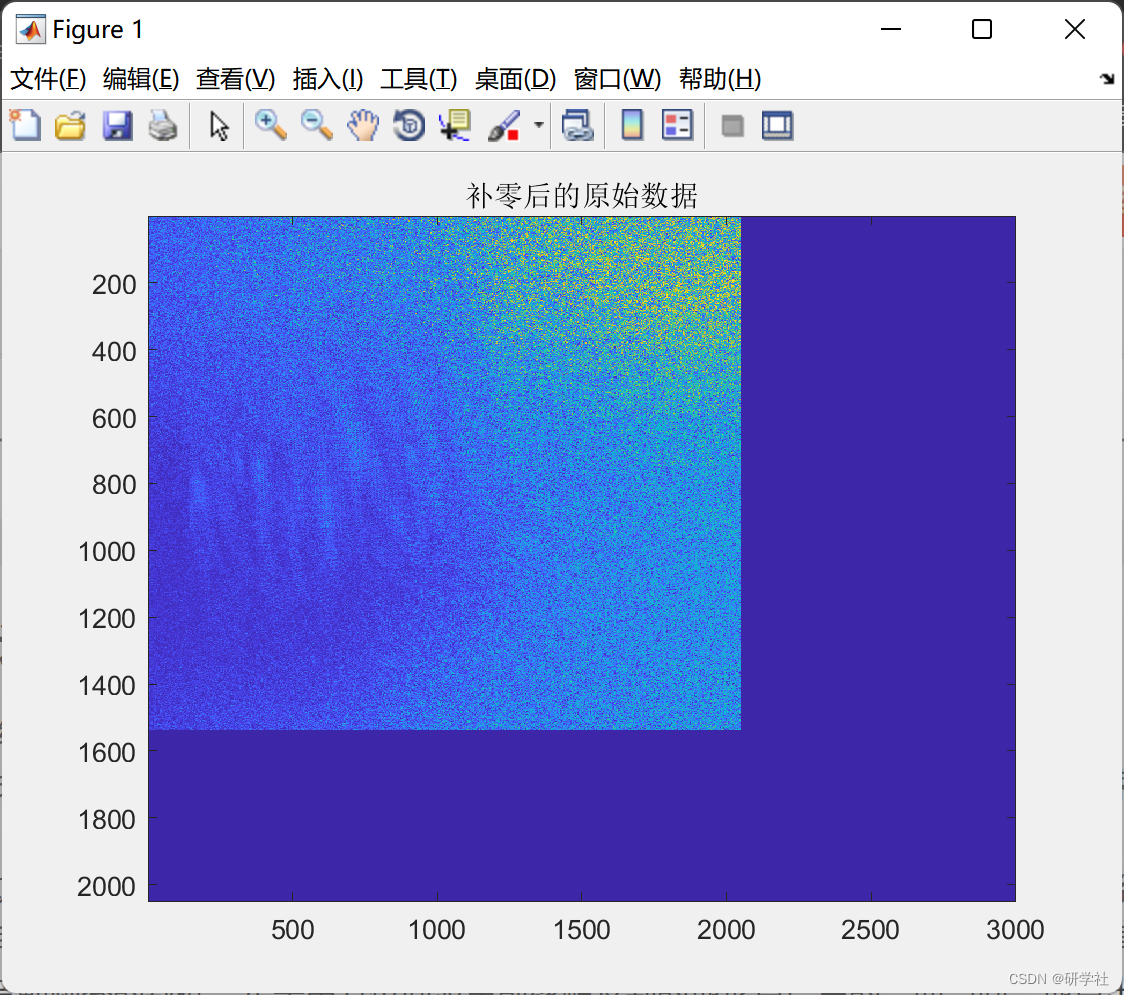
figure;
imagesc(abs(s_echo));
title('补零后的原始数据'); % 补零后的原始回波数据(未处理)的幅度图像
%}
%%
% --------------------------------------------------------------------
% 距离(方位)向时间,频率相关定义
% --------------------------------------------------------------------
% 距离
tr = 2*R0/c + ( -Nrg/2 : (Nrg/2-1) )/Fr; % 距离时间轴
fr = ( -NFFT_r/2 : NFFT_r/2-1 )*( Fr/NFFT_r ); % 距离频率轴
% 方位
ta = ( -Naz/2: Naz/2-1 )/Fa; % 方位时间轴
fa = fnc + fftshift( -NFFT_a/2 : NFFT_a/2-1 )*( Fa/NFFT_a ); % 方位频率轴
% 生成距离(方位)时间(频率)矩阵
tr_mtx = ones(Naz,1)*tr; % 距离时间轴矩阵,大小:Naz*Nrg
ta_mtx = ta.'*ones(1,Nrg); % 方位时间轴矩阵,大小:Naz*Nrg
fr_mtx = ones(Naz,1)*fr; % 距离频率轴矩阵,大小:Naz*Nrg
fa_mtx = fa.'*ones(1,Nrg); % 方位频率轴矩阵,大小:Naz*Nrg
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]《合成孔径雷达成像——算法与实现》 ,(美)卡明等著;洪文等译;电子工业出版社;
[2]《合成孔径雷达——系统与信号处理》 ,(美)柯兰德等著;韩传钊等译;电子工业出
版社






)













:反思证据及当前问题解决)