给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
大根堆
这段代码是使用大根堆(max-heap)来解决问题的思路。
在这个解决方案中,通过将整个 nums 数组初始化为一个大根堆 priority_queue<int> pq(nums.begin(), nums.end())。大根堆会自动将较大的元素放在堆顶部。
然后,通过循环 while (--k) 来逐个排除前k-1个最大的元素,即每次都执行 pq.pop() 弹出堆顶的元素。
最后,返回 pq.top(),即堆中剩余的最大元素,也就是第k大的元素。
因此,该代码使用大根堆的性质在O(nlogn)的时间复杂度下找到了第k大的元素。

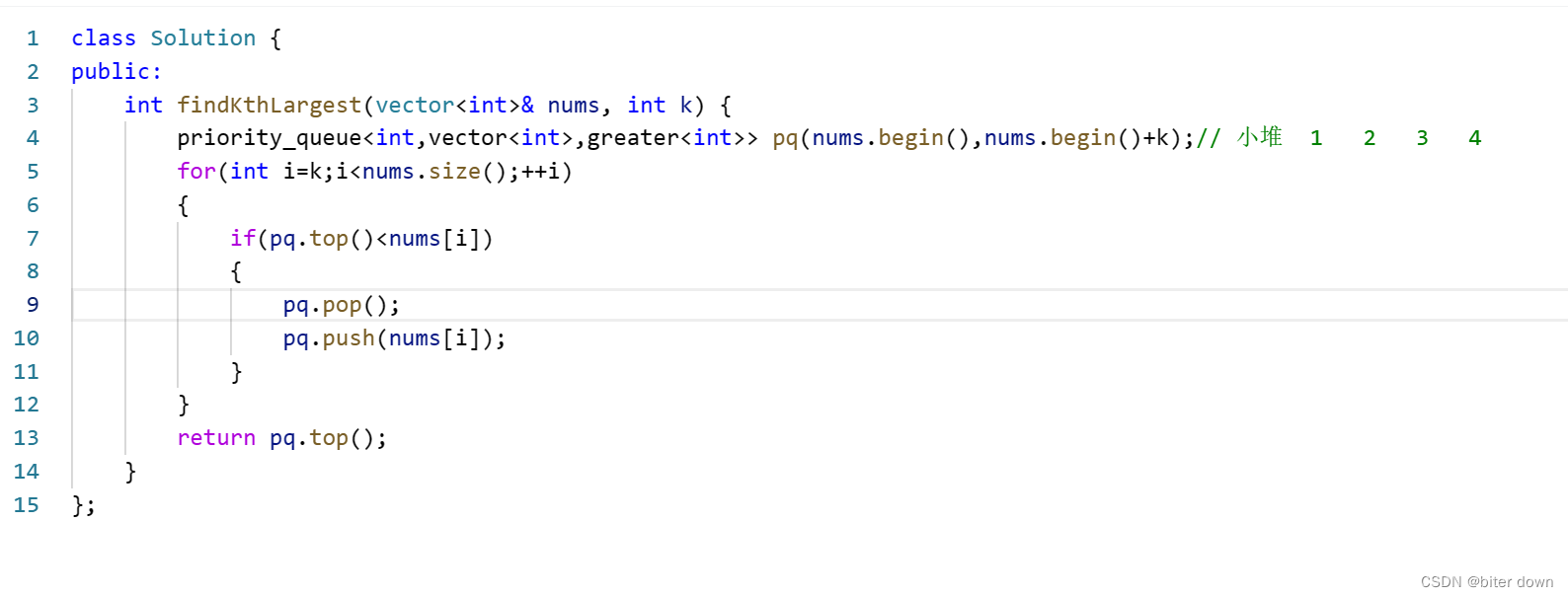
小根堆
在这段代码中,将priority_queue pq初始化为nums.begin() + k原因是为了确保初始的priority_queue中包含第k大的元素。
在此代码中,priority_queue被用作最小堆(较小的元素位于顶部)。想法是始终维护一个最小堆,其中包含目前为止遇到的k个最大元素。
通过使用nums.begin() + k来初始化priority_queue,会将nums中的前k大元素插入到priority_queue中。这确保了第k大的元素也存在于最小堆中。
随后,在迭代nums的剩余元素时,如果找到了更大的元素,则它将替换掉最小的元素。这确保在处理完所有元素后,priority_queue pq将包含nums中遇到的k个最大元素,并且其中最小的元素将位于顶部(pq.top())。
![[腾讯云Cloud Studio实战训练营]无门槛使用GPT+Cloud Studio辅助编程完成Excel自动工资结算](http://pic.xiahunao.cn/[腾讯云Cloud Studio实战训练营]无门槛使用GPT+Cloud Studio辅助编程完成Excel自动工资结算)




TomcatStarter)











)

,搭建方案)