图像二值化阈值调整——Triangle算法，Maxentropy方法

一. Triangle方法

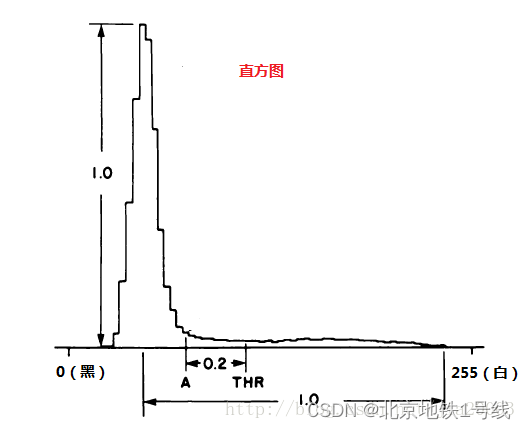
算法描述：三角法求分割阈值最早见于Zack的论文《Automatic measurement of sister chromatid exchange frequency》主要是用于染色体的研究，该方法是使用直方图数据，基于纯几何方法来寻找最佳阈值，它的成立条件是假设直方图最大波峰在靠近最亮的一侧，然后通过三角形求得最大直线距离，根据最大直线距离对应的直方图灰度等级即为分割阈值，图示如下：

三角几何化的过程。首先找到直方图中灰度值最高的一点并判别亮暗，然后找到最左边点，两点连接一条直线，求直方图上离直线最远的点，设置该点的灰度值为阈值。

有时候最大波峰对应位置不在直方图最亮一侧，而在暗的一侧，这样就需要翻转直方图，翻转之后求得值，用255减去即得到为阈值T。扩展情况的直方图表示如下：

算法特点：适用于单峰。这点和OTSU算法有很大区别，OTSU适用于双峰。

cv2中有三角分割的算法，直接使用即可。

import cv2
import matplotlib.pylab as pltdef main():img = cv2.imread('6.jpg', 0)ret, thresh1 = cv2.threshold(img, 0, 255, cv2.THRESH_TRIANGLE)print(ret)  # 结果是151.0titles = ['Original Image', 'After Binarization']images = [img, thresh1]for i in range(2):plt.subplot(1, 2, i + 1)plt.imshow(images[i], 'gray')plt.title(titles[i])plt.xticks([])plt.yticks([])plt.show()main()

二. Maxentropy方法

最大熵阈值分割法和OTSU算法类似，假设将图像分为背景和前景两个部分。熵代表信息量，图像信息量越大，熵就越大，最大熵算法就是找出一个最佳阈值使得背景与前景两个部分熵之和最大。

给定一个大小为M*N的图像，直方图中所有矩形框所代表的数值之和，即为图像中的像素数量，设像素值i的像素在图中有 $h(i)$ 个，即：

$\sum_{i=0}^{K-1}h(i)=MN$

相对应的归一化直方图表示为：

$p(i)=\frac{h(i)}{MN}$

其中0<=i<K。通常被解释为一个随机过程的概率分布或概率密度函数， $p(i)$ 表示的是图像中像素灰度值为i所出现的概率。i的累积概率值为1，即概率分布p必须满足以下关系：

$\sum_{i=0}^{K-1}p(i)=1$

与累积概率所对应的累积直方图H是一个离散的分布函数P()（通常也称为累积分布函数或cdf），P（i）表示像素值小于等于i的概率：

$P(i)=\sum_{j=0}^{i}p(j)$

在图像处理中，灰度图的熵定义如下：

$Entropy=-\sum_{i=0}^{K-1}p(i)log_2p(i)$

因为 $p(i)\in \left [ 0,1 \right ]$ ，所以 $log_2p(i)<0,-log_2p(i)>0$ 。

利用图像熵为准则进行图像分割有一定历史了，学者们提出了许多以图像熵为基础进行图像分割的方法。以下介绍一种由Kapuret al提出来，现在仍然使用较广的一种图像熵分割方法。

给定一个特定的阈值q(0<=q<K-1)，对于该阈值所分割的两个图像区域C0，C1，这两部分的熵可写为：

$H(0)=- \sum_{i=0}^{q}\frac{p(i)}{P_0(q)}log_2\frac{p(i)}{P_0(q)}$

$H(1)=- \sum_{i=q+1}^{K-1}\frac{p(i)}{P_1(q)}log_2\frac{p(i)}{P_1(q)}$

其中： $P_0(q)=\sum_{i=0}^{q}p(i)$ ， $P_1(q)=\sum_{i=q+1}^{K-1}p(i)$ ， $P_0(q)+P_1(q)=1$ 。

图像总熵为： $H_q=H(0)+H(1)$ 。现在就是要遍历q(0<=q<K-1)，使得Hq最大。

为了计算方便，对H（0）和H（1）的表达式进行优化：

$H(0)=- \sum_{i=0}^{q}\frac{p(i)}{P_0(q)}\left ( log_2p(i)-log_2P_0(q) \right ) =-\frac{1}{P_0(q)}[\sum_{i=0}^{q}p(i)log_2p(i)-log_2P_0(q)\sum_{i=0}^{q}p(i)]$

得到 $H(0)=\frac{1}{P_0(q)}S_0(q)+log_2P_0(q)$

同理 $H(1)=\frac{1}{P_1(q)}S_1(q)+log_2P_1(q)$

其中 $S_0(q)=-\sum_{i=0}^{q}p(i)log_2p(i)$ ， $S_1(q)=-\sum_{i=q+1}^{K-1}p(i)log_2p(i)$ 。

import cv2
import matplotlib.pylab as plt
import numpy as np
import mathdef calcGrayHist(image):rows, cols = image.shape[:2]grayHist = np.zeros([256], np.uint64)for row in range(rows):for col in range(cols):grayHist[image[row][col]] += 1return grayHistdef thresh_entropy(image):rows, cols = image.shape# 求灰度直方图grayHist = calcGrayHist(image)# 归一化灰度直方图，即概率直方图normGrayHist = grayHist / float(rows*cols)  # 就是上面讲的p(i)# 1.计算累加直方图zeroCumuMoment = np.zeros([256], np.float32) # 就是上面讲的P(i)for i in range(256):if i == 0:zeroCumuMoment[i] = normGrayHist[i]else:zeroCumuMoment[i] = zeroCumuMoment[i-1] + normGrayHist[i]# 2.计算各个灰度级的熵entropy = np.zeros([256], np.float32)  # 就是上面讲的S_0(q)for i in range(256):if i == 0:if normGrayHist[i] == 0:  # 0log2_0是0，但是对数在0处没有定义entropy[i] = 0else:entropy[i] = -normGrayHist[i] * math.log2(normGrayHist[i])else:if normGrayHist[i] == 0:entropy[i] = entropy[i-1] # 0log2_0是0，但是对数在0处没有定义else:entropy[i] = entropy[i-1] - normGrayHist[i] * math.log2(normGrayHist[i])# 3.找阈值fT = np.zeros([256], np.float32)ft1, ft2 = 0.0, 0.0totalEntropy = entropy[255]for i in range(255):# 找最大值ft1 = entropy[i] / zeroCumuMoment[i] + math.log2(zeroCumuMoment[i])ft2 = (entropy[255] - entropy[i]) / (1 - zeroCumuMoment[i]) + math.log2(1 - zeroCumuMoment[i])fT[i] = ft1 + ft2# 找最大值的索引，作为得到的阈值print(fT)threshLoc = np.where(fT == np.max(fT))thresh = threshLoc[0][0]# 阈值处理threshold = np.copy(image)threshold[threshold>thresh] = 255threshold[threshold<=thresh] = 0return thresh, thresholddef main():img = cv2.imread("6.jpg", 0)thresh, threshImg = thresh_entropy(img)print(thresh) # 结果是104.0titles = ['Original Image', 'After Binarization']images = [img, threshImg]for i in range(2):plt.subplot(1, 2, i + 1)plt.imshow(images[i], 'gray')plt.title(titles[i])plt.xticks([])plt.yticks([])plt.show()main()