1.车尔尼有一个数组 nums ,它只包含 正 整数,所有正整数的数位长度都 相同 。
两个整数的 数位不同 指的是两个整数 相同 位置上不同数字的数目。
请车尔尼返回 nums 中 所有 整数对里,数位不同之和。
示例 1:
输入:nums = [13,23,12]
输出:4
解释:
计算过程如下:
- 13 和 23 的数位不同为 1 。
- 13 和 12 的数位不同为 1 。
- 23 和 12 的数位不同为 2 。
所以所有整数数对的数位不同之和为 1 + 1 + 2 = 4
class Solution {
public:
long long sumDigitDifferences(vector<int>& nums) {
long long ans = 0; // 初始化答案为0
// cnt 是一个二维数组,每个元素是一个大小为10的数组
// cnt[i][d] 表示在第 i 位上数字为 d 的个数
vector<array<int, 10>> cnt(to_string(nums[0]).length());
// 遍历 nums 数组
for (int k = 0; k < nums.size(); k++) {
int x = nums[k]; // x 是当前处理的整数
// 遍历 x 的每一位
for (int i = 0; x; x /= 10, i++) {
int d = x % 10; // 取出 x 的最低位数字 d
// 更新答案 ans
// k - cnt[i][d] 表示第 i 位上数字为 d 的个数与当前位置 k 的差值
ans += k - cnt[i][d]++;
}
}
return ans; // 返回最终的答案
}
};
-
初始化变量和数据结构:
ans初始化为 0,用来存储最终的结果,即所有整数对的数位不同之和。cnt是一个二维数组,大小为to_string(nums[0]).length(),即第一个整数的位数。每个cnt[i]是一个大小为 10 的数组,用来统计每个位置上数字出现的次数。
-
遍历整数数组
nums:- 对于数组中的每个整数
nums[k],进行处理。
- 对于数组中的每个整数
-
处理每个整数
x:- 使用一个内部循环,不断取出
x的最低位数字d,直到x变为 0。 x % 10得到x的最低位数字d。x /= 10将x右移一位,继续处理下一位数字。
- 使用一个内部循环,不断取出
-
更新答案
ans:- 对于每个数字
d在第i位上出现,更新ans:k - cnt[i][d]表示当前位置k减去第i位上数字为d的个数。cnt[i][d]++更新cnt[i][d],表示第i位上数字为d的个数增加了一个。
- 对于每个数字
-
返回结果:
- 返回累计的
ans,即所有整数对的数位不同之和。
- 返回累计的
2. 如果数组的每一对相邻元素都是两个奇偶性不同的数字,则该数组被认为是一个 特殊数组 。
周洋哥有一个整数数组 nums 和一个二维整数矩阵 queries,对于 queries[i] = [fromi, toi],请你帮助周洋哥检查子数组 nums[fromi..toi] 是不是一个 特殊数组 。
返回布尔数组 answer,如果 nums[fromi..toi] 是特殊数组,则 answer[i] 为 true ,否则,answer[i] 为 false 。
示例 1:
输入:nums = [3,4,1,2,6], queries = [[0,4]]
输出:[false]
解释:
子数组是 [3,4,1,2,6]。2 和 6 都是偶数。
class Solution {
public:
vector<bool> isArraySpecial(vector<int>& nums, vector<vector<int>>& queries) {
int k=queries.size();
int q[100000] = {0};
q[0]=1;
for (int i = 1; i < nums.size(); ++i) {
if ((nums[i] % 2) == (nums[i - 1] % 2))
q[i] = q[i - 1] + 1;
else
q[i] = q[i - 1];
}
vector<bool> answer;
for (int i = 0; i <k; i++) {
if (q[queries[i][0]] == q[queries[i][1]]) {
answer.push_back(true);
}
else
answer.push_back(false);
}
return answer;
}
};
给你两个整数 numBottles 和 numExchange 。
numBottles 代表你最初拥有的满水瓶数量。在一次操作中,你可以执行以下操作之一:
- 喝掉任意数量的满水瓶,使它们变成空水瓶。
- 用
numExchange个空水瓶交换一个满水瓶。然后,将numExchange的值增加 1 。
注意,你不能使用相同的 numExchange 值交换多批空水瓶。例如,如果 numBottles == 3 并且 numExchange == 1 ,则不能用 3 个空水瓶交换成 3 个满水瓶。
返回你 最多 可以喝到多少瓶水。
示例 1:

输入:numBottles = 13, numExchange = 6 输出:15 解释:上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值,以及累计喝掉的水瓶数量。
class Solution {
public:
int maxBottlesDrunk(int numBottles, int numExchange) {
// ans:答案
// emp:目前有的空瓶数
int ans = 0, emp = 0;
while (true) {
// 把所有水喝完
ans += numBottles;
emp += numBottles;
numBottles = 0;
if (emp >= numExchange) {
// 空瓶足够,进行一次兑换
emp -= numExchange;
numBottles++;
numExchange++;
} else {
// 空瓶不够了,无法获得更多瓶子,退出模拟
break;
}
}
return ans;
}
};
由于每 numExchange 个空瓶才能换一瓶,且每次兑换 numExchange 都会加一,所以只要 numExchange 至少为 2,则每次兑换都会至少“损失”一个瓶子。一开始一共只有 numBottles 个瓶子,显然至多 numBottles 次兑换之后就没有瓶子了。
4
给你一个大小为 m x n 的二维矩阵 grid 。你需要判断每一个格子 grid[i][j] 是否满足:
- 如果它下面的格子存在,那么它需要等于它下面的格子,也就是
grid[i][j] == grid[i + 1][j]。 - 如果它右边的格子存在,那么它需要不等于它右边的格子,也就是
grid[i][j] != grid[i][j + 1]。
如果 所有 格子都满足以上条件,那么返回 true ,否则返回 false 。
示例 1:
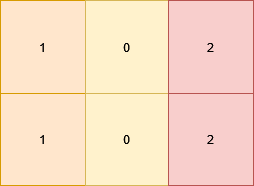
输入:grid = [[1,0,2],[1,0,2]]
输出:true
解释:
class Solution {
public:
bool satisfiesConditions(vector<vector<int>>& grid) {
int m,n;
m=grid.size();
n=grid[0].size();
for(int i=0;i<m-1;i++)
{
for(int j=0;j<=n-1;j++)
{
if(grid[i][j]!=grid[i+1][j])
return false;
}
}
for(int j=0;j<n-1;j++)
{
if(grid[0][j]==grid[0][j+1])
{
return false;
}
}
return true;
}
};
对于每个格子 grid[i][j],它需要与它下面的格子 grid[i+1][j] 相等。这一部分代码通过两层循环实现:
for (int i = 0; i < m - 1; ++i)
{
for (int j = 0; j < n; ++j)
{
if (grid[i][j] != grid[i+1][j])
{
return false;
} } }
在第一层循环中,遍历每一行 i,第二层循环遍历该行的每一列 j。如果发现 grid[i][j] 不等于 grid[i+1][j],即当前格子与下面的格子不相等,直接返回 false。
条件二检查: 对于每个格子 grid[i][j],它需要与其右边的格子 grid[i][j+1] 不相等。这部分代码如下:
for (int j = 0; j < n - 1; ++j)
{
if (grid[0][j] == grid[0][j+1])
{
return false; } }
这里只需遍历第一行 grid[0] 的每一列 j,检查相邻的两个格子 grid[0][j] 和 grid[0][j+1] 是否相等。如果有任何一对相邻格子相等,即返回 false。
返回结果: 如果两个条件都满足,即所有格子都满足要求,则返回 true。


)





论文解读)



)




安装问题解决)

)