视频链接
如果Optimization失败的时候,怎么把梯度下降做的更好?
只考虑这种情况,不考虑overfitting
局部最小值(local minima)和鞍点(saddle point)
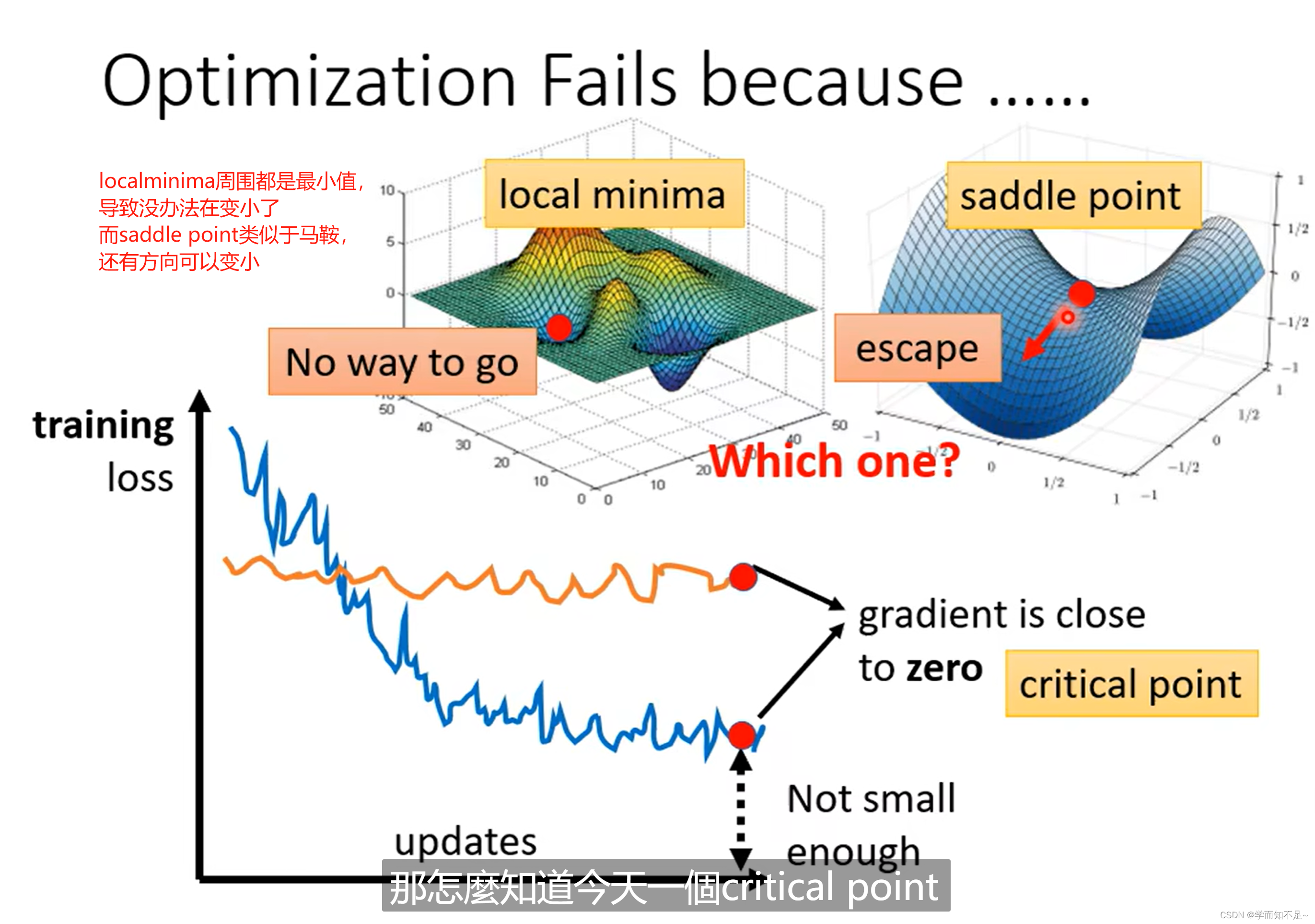
为什么Optimization会失败?
可能是gradient为0,导致梯度下降不继续工作了,即critical point(临界点)为0,原因要么是local minima,要么是saddle point(像马鞍一样的面,所以被称为鞍点)
数学解释
泰勒展开
使用泰勒级数近似法来逼近某一个复杂函数的近似值
海塞矩阵

海塞矩阵
由于在临界点的时候,gradient为0,所以我们只需要考虑后面那一项的形状即可知道当前处于什么样的情况

假设v = θ - θ’
我们可以通过v的值来判断当前值θ’的类型
即如果所有的v都是正的,则L(θ) > L(θ’),则为local minima
如果所有v都是负的,则L(θ) < L(θ’),则为local maxima
如果v有正有负,则为saddle point
但是我们没办法算出所有的v,所以上面的方法是理论上可行
但是有个结论是我们可以通过海塞矩阵H的特征值来判断θ’的类型:
如果所有的特征值为正,则为local minima
所有特征值为负,则为local maxima
特征值有正有负,则为saddle point
如图:

例子
分别算出g和H,然后算出H的特征值,即可知道某个临界点是属于什么类型
特征值的计算需要学习一下
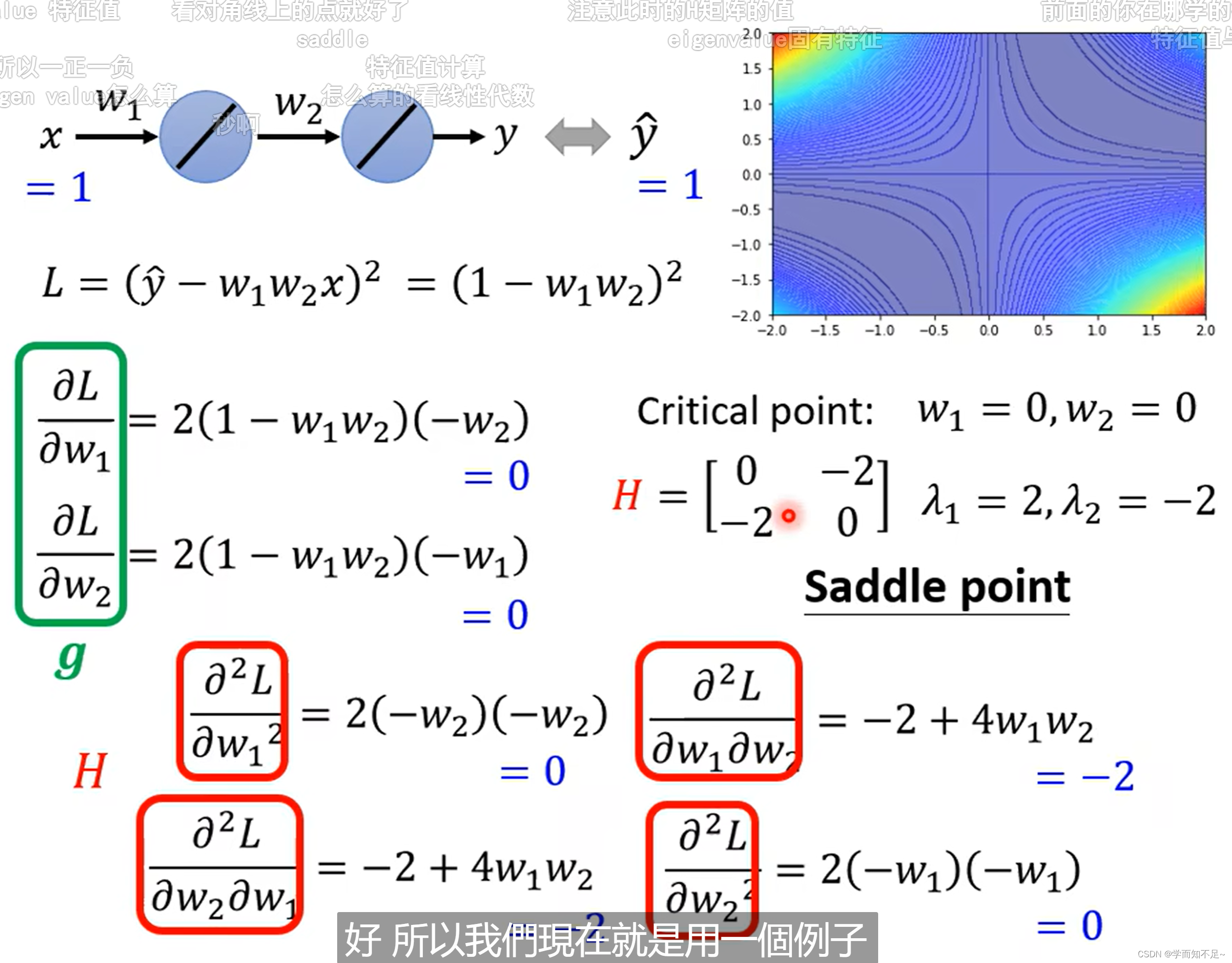
如果是saddle point,可以通过海塞矩阵H知道要更新的方向,具体:
通过找到一个能够使海塞矩阵所在项值变小的u,即可确定要更新的方向
其中u是特征向量,通过特征值找出来

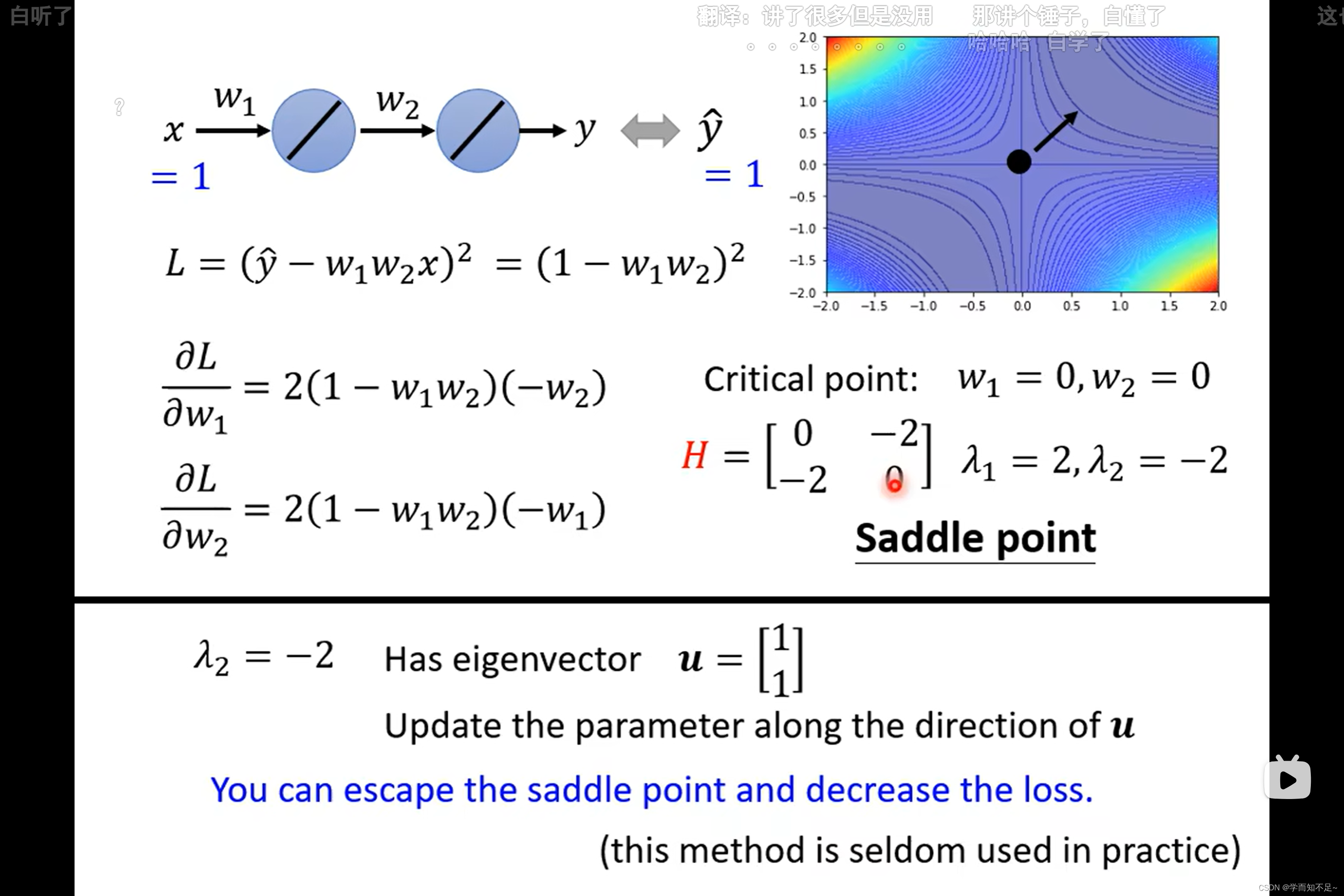
然而,实际上由于计算海塞矩阵H太过复杂,一般都不适用这种方式来找到更新方向
saddle point和local minima哪个更常见?
结论:在低维度的情况下是local minima,可能在高维度上实际上是saddle point
批次(batch)和动量(Momentum)
batch批次
batch:批次,即把所有的数据分批次
epoch:遍历一次所有的batch
shuffle:遍历一次epoch,打乱一次顺序
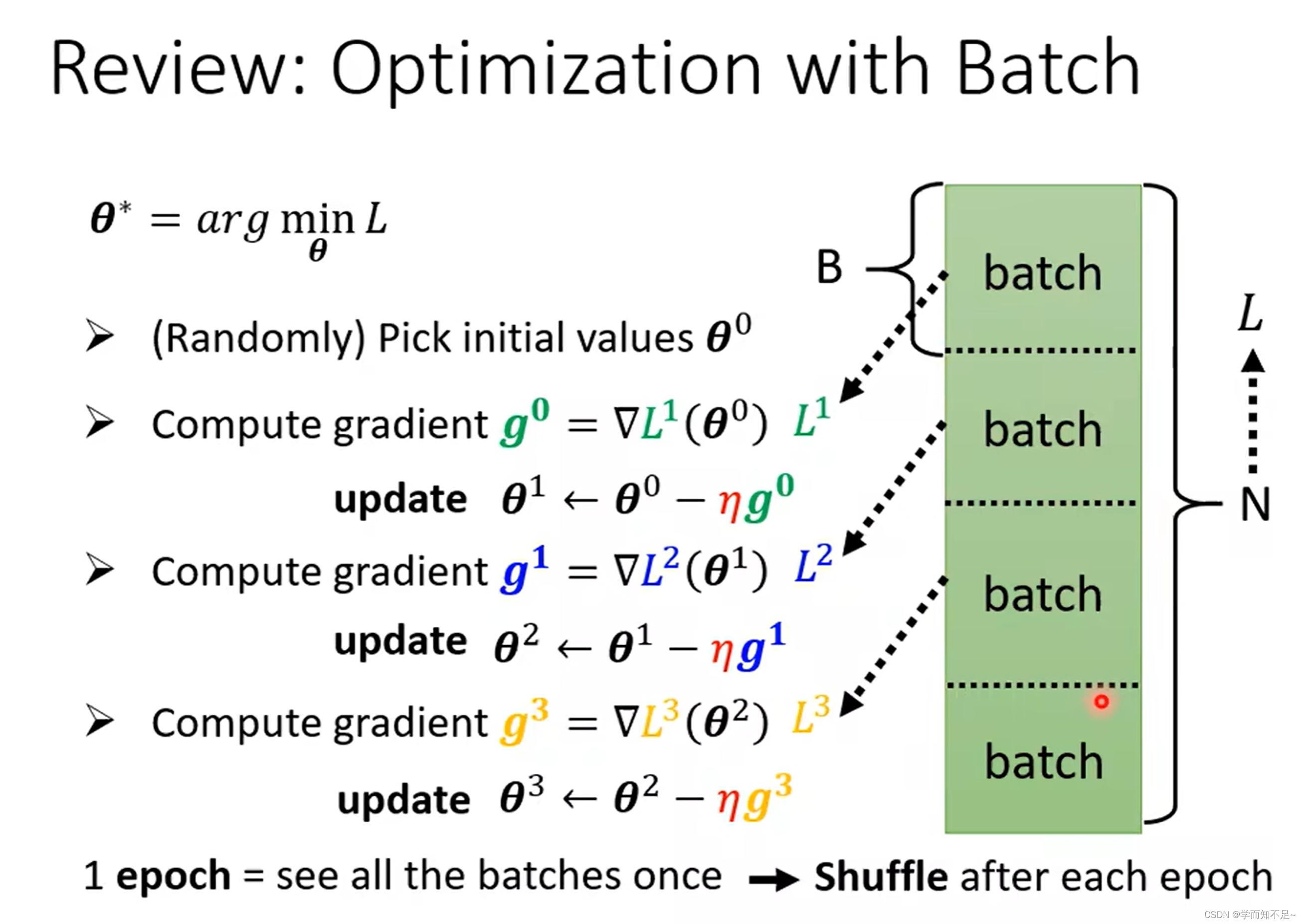
为什么要用batch,使用小的batch Size还是大的batch Size

然而,考虑到并行运算,实际上遍历大的batch,未必就比小的时间长
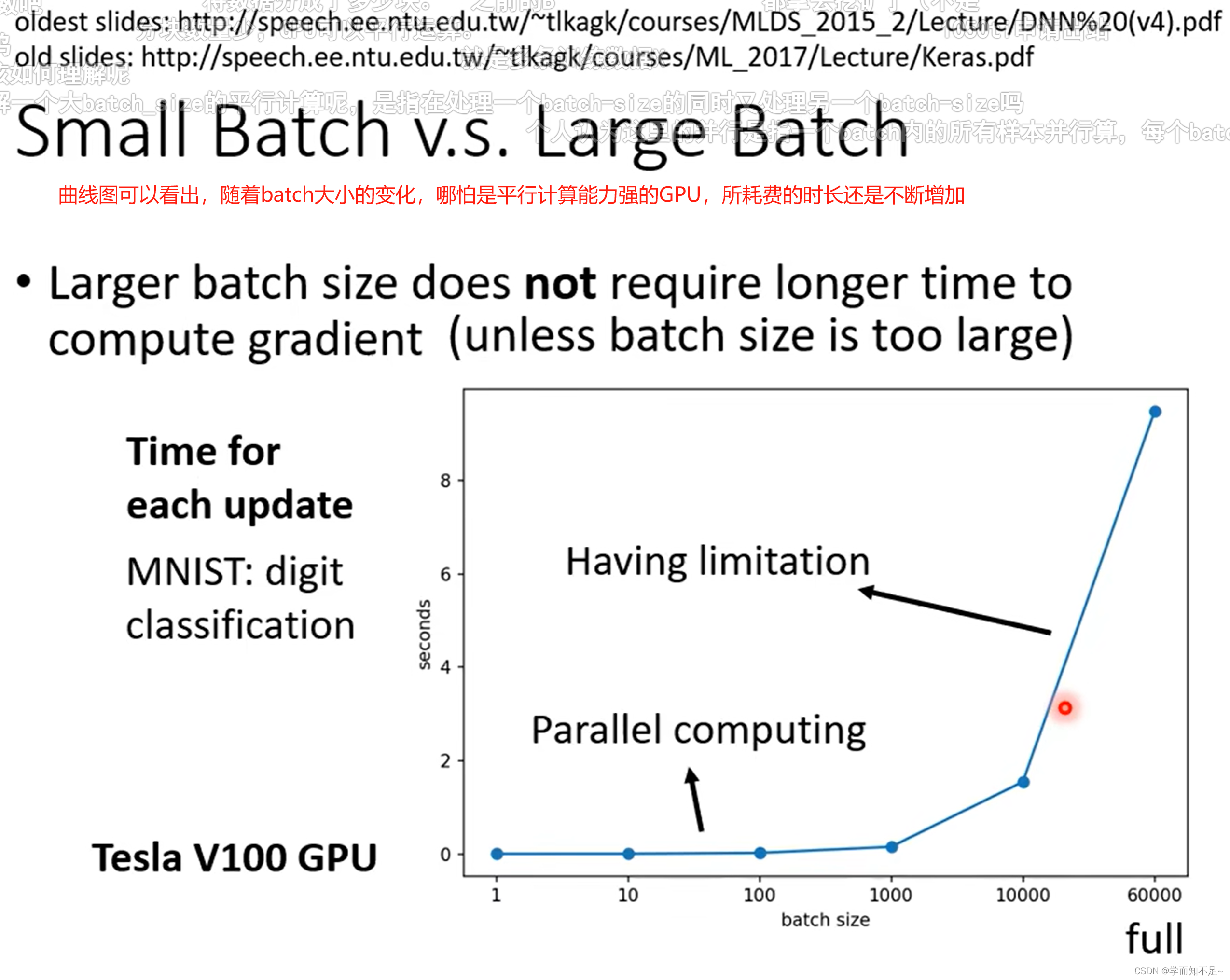
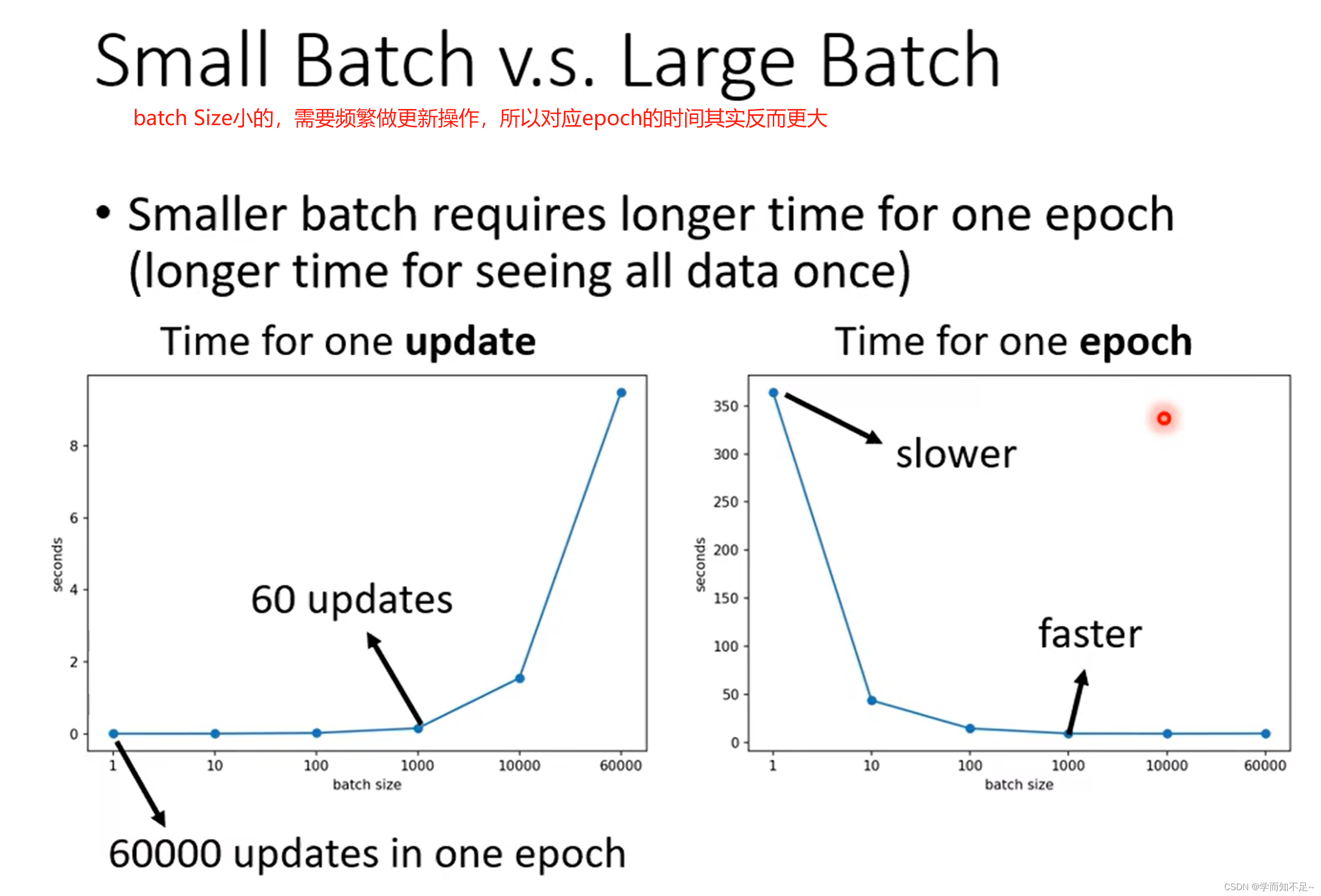
虽然batch Size越大,所花的时间越少,看上去选择batch Size大的会比较合适。然而实验证明batch Size小的虽然noisy,但是有利于我们的训练,原因是因为大的batch Size可能会有Optimization的问题
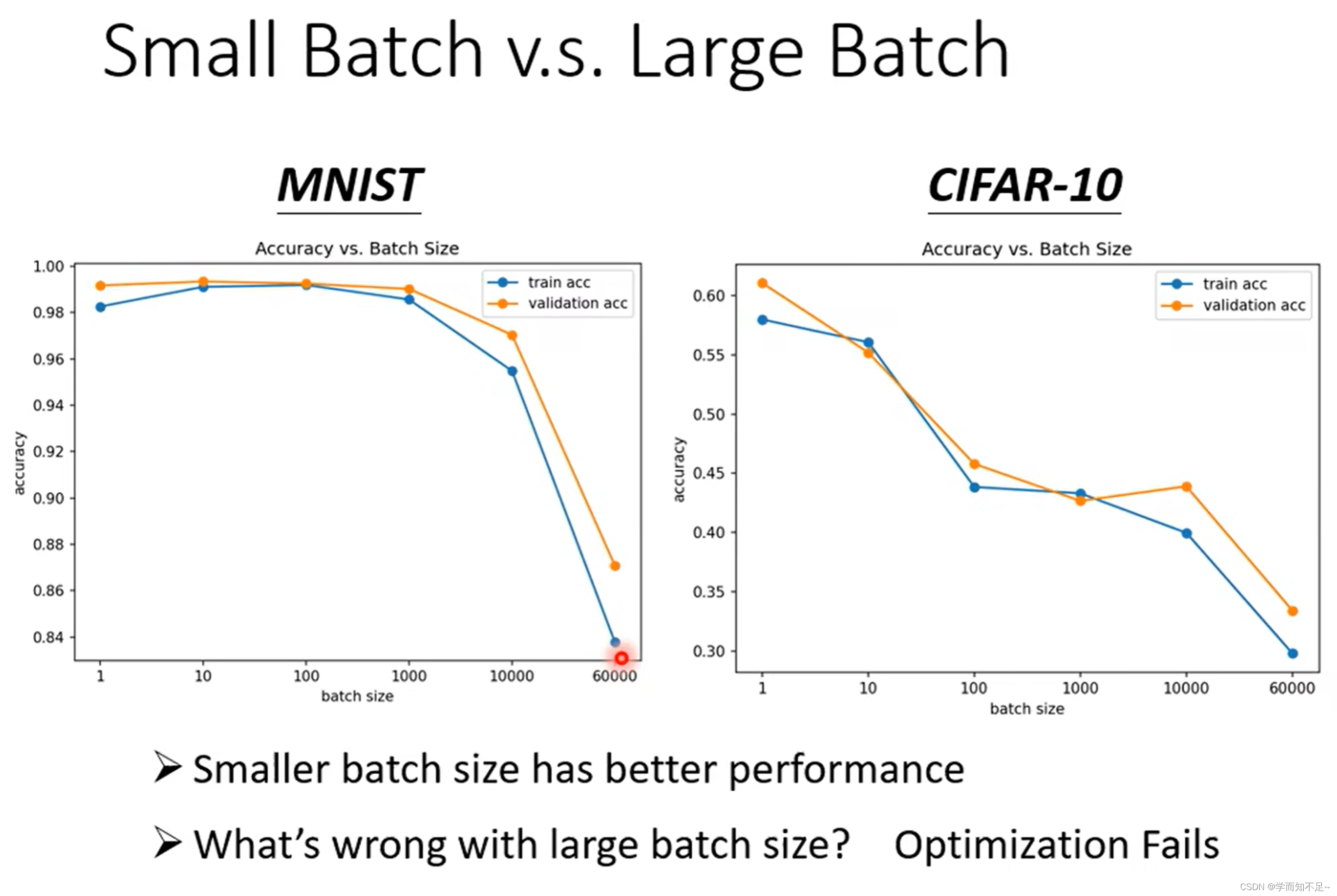
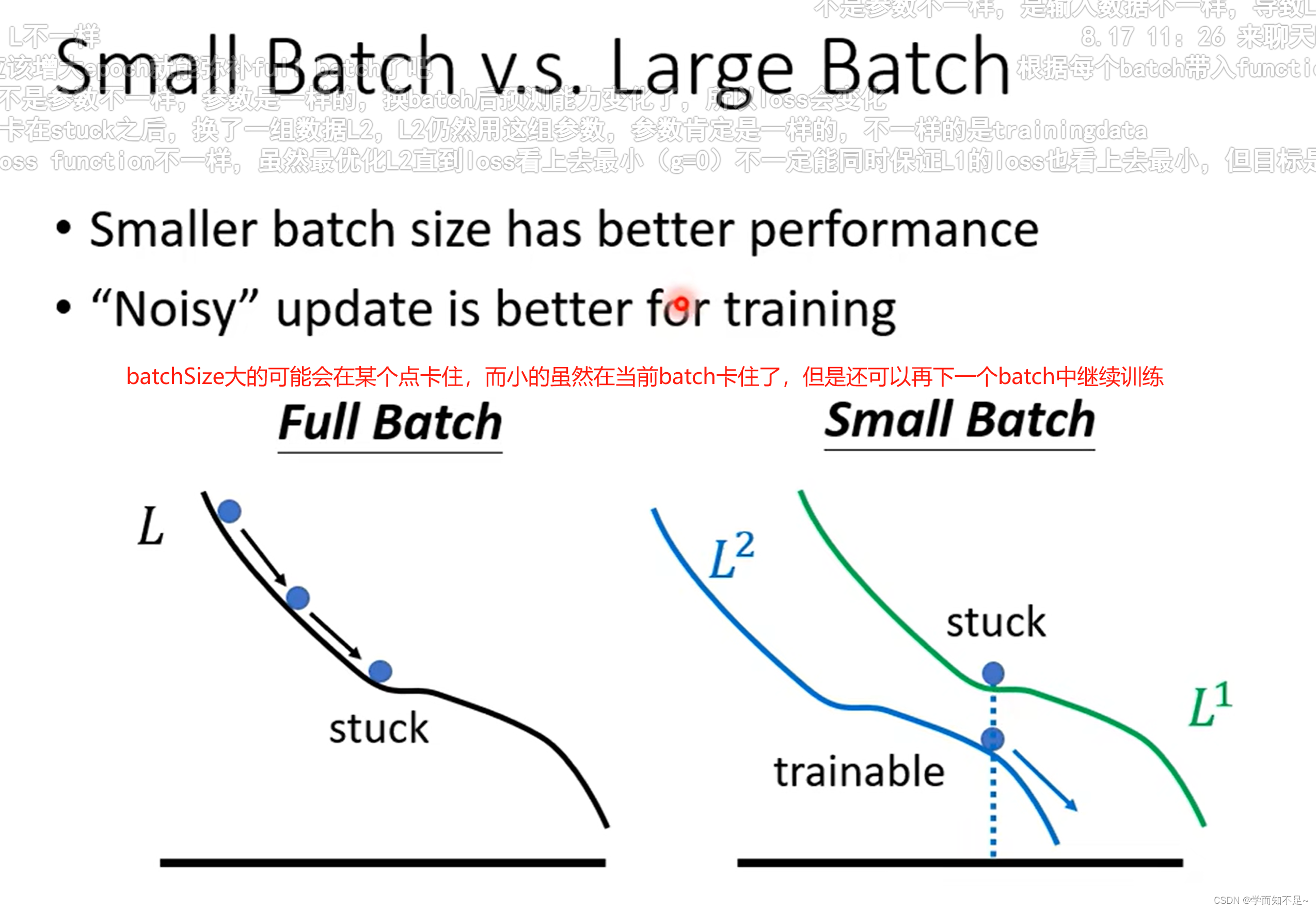
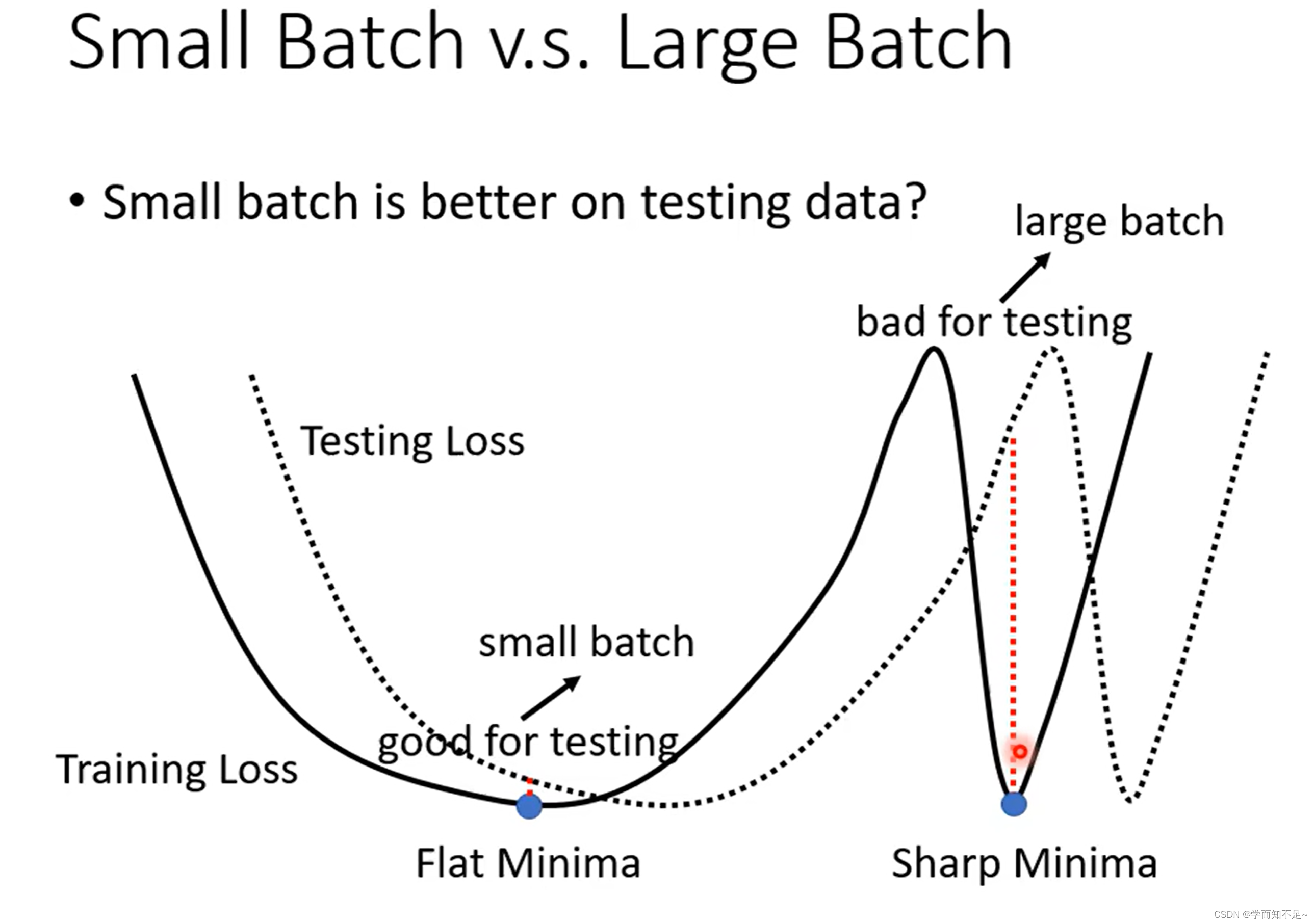
batch Size 小的在测试数据上表现比大的好吗?
由于batch Size小的对应的Loss曲线更加曲折,而大的对应的曲线更加平缓;
一个直观的想法就是当训练数据和测试数据有一定偏差时,通过训练数据得到的曲线,越平缓,与测试数据的Loss就越小
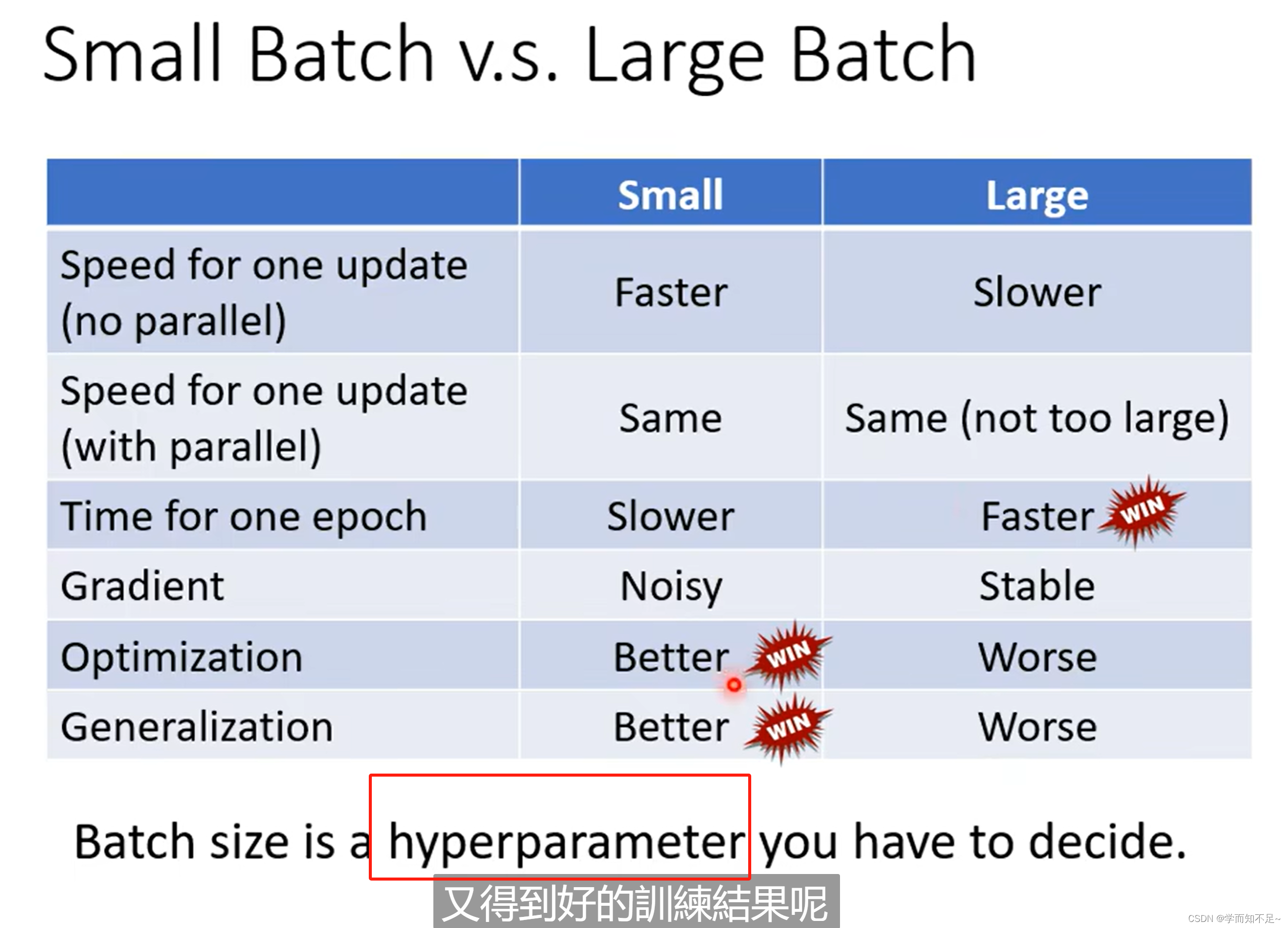
结论
batch Size大和小都各自有各自的优点,所以这个就成了一个超参数,通过自己调整来得到更好的训练结果,许多文章都在探讨这个问题
Momentum动量
在实际的物理世界中,假设一个球从高处滑落,哪怕到达一个局部最低点,因为有动力的缘故,球也有可能翻越这个local minima继续往下走。
由这个想法引申出一个问题——能否将这个概念引入到梯度下降中呢?
只考虑gradient的方向:
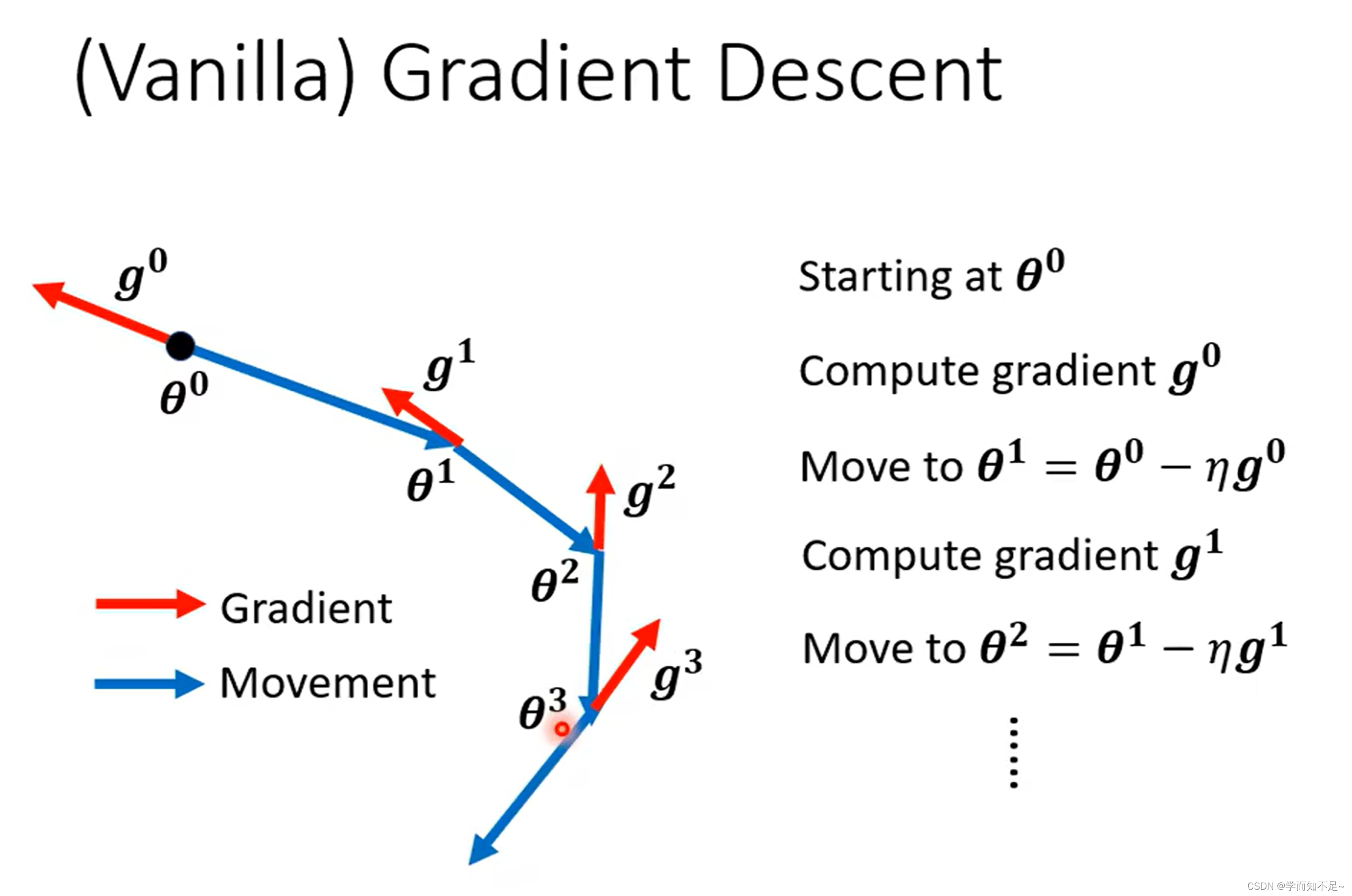
gradient的方向加上movement的方向:
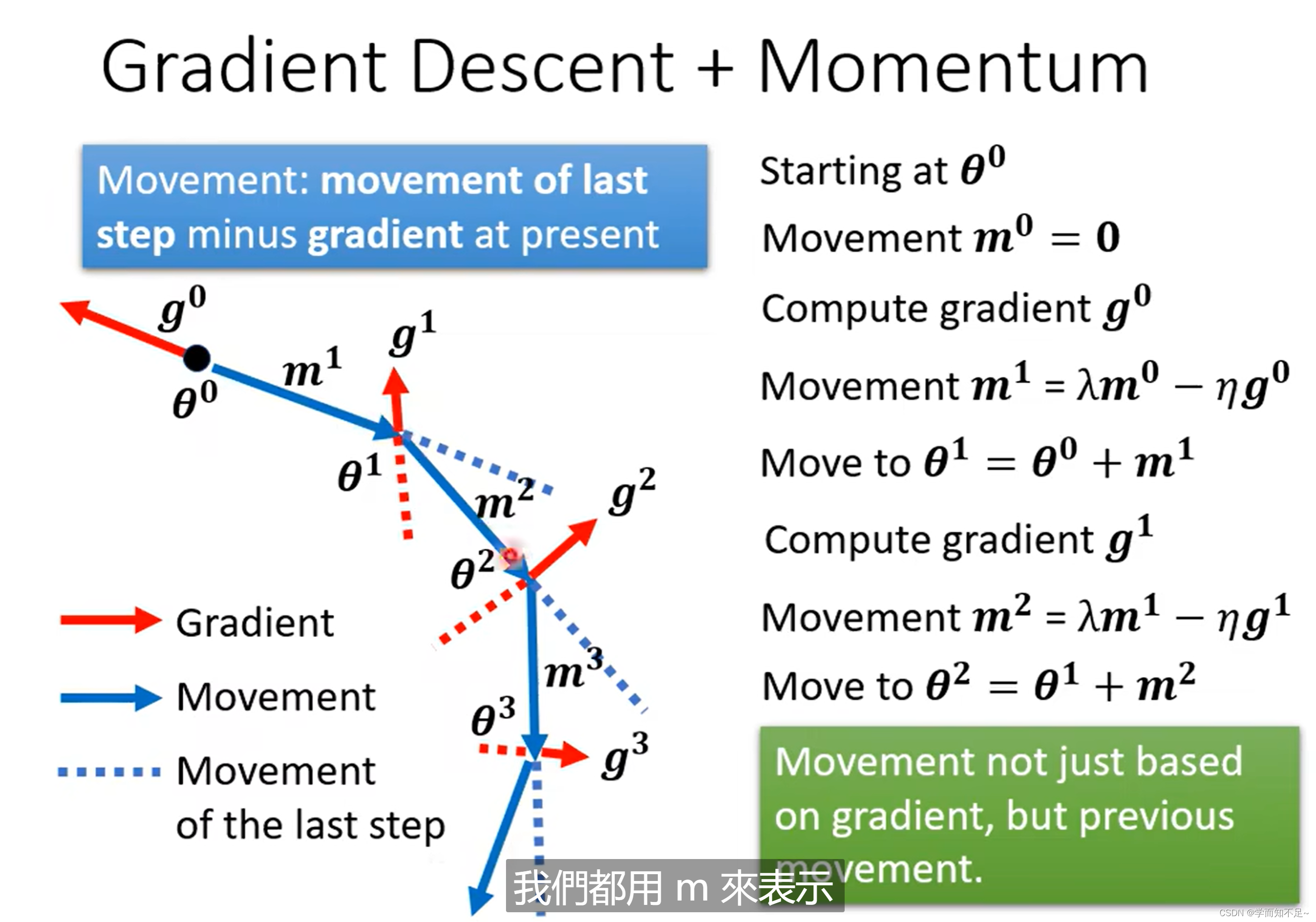


结论
实际上就是考虑了之前运动的方向,与当前算出的gradient做了个角度的修改,从而减少了local minima的概率
自动调整学习率(learning rate)
其实,临界点问题(critical point)并不一定是训练过程中最大的阻碍
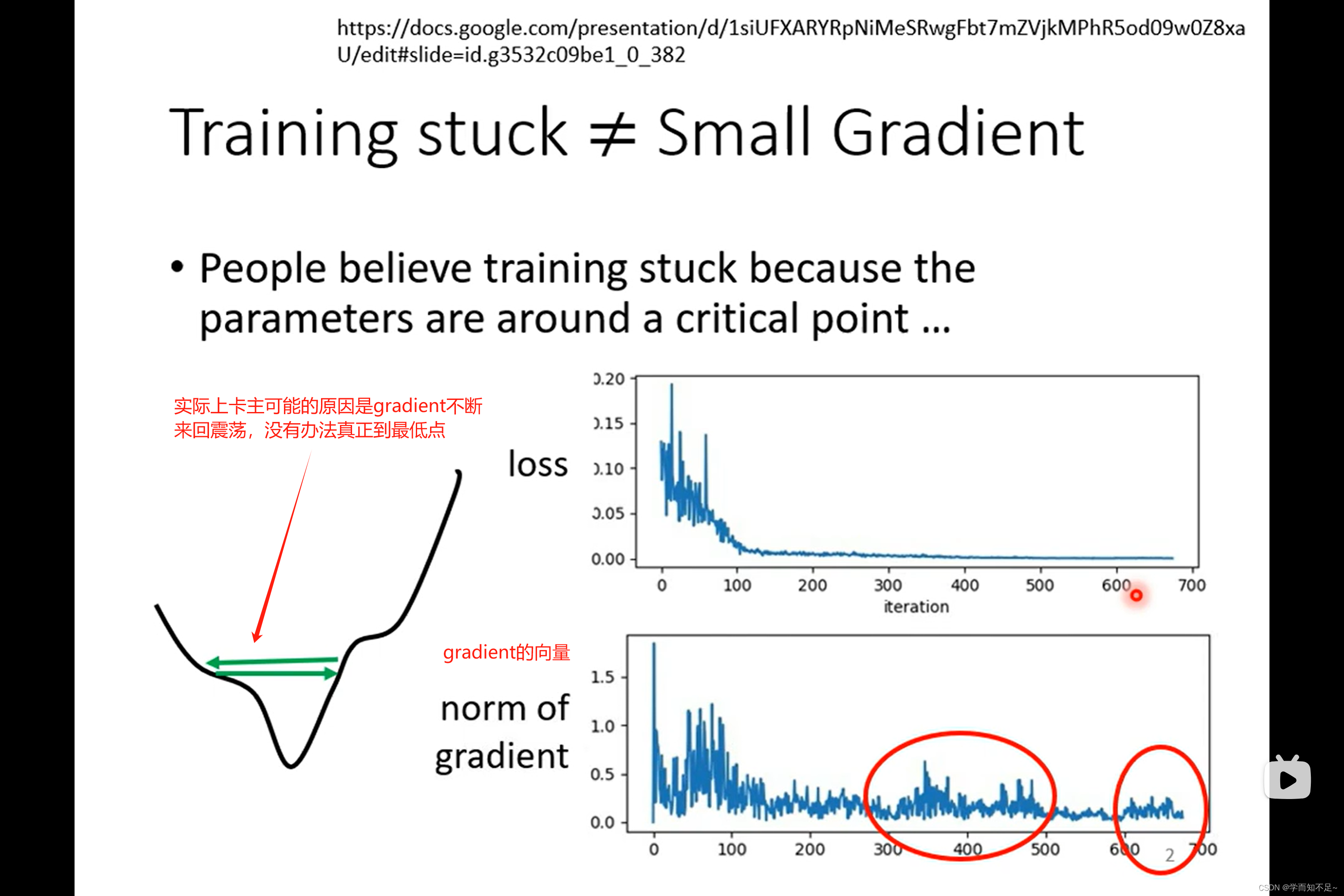
同样一个函数如凸函数,当learning rate设的很大的时候,他会来回震荡导致Loss一直减小不了
当learning rate设的很小时,虽然不会在震荡,但是在平坦的地方下降太过缓慢,导致永远都走不到最小的Loss;所以learning rate必须根据不同的Gradient,调整不同的值
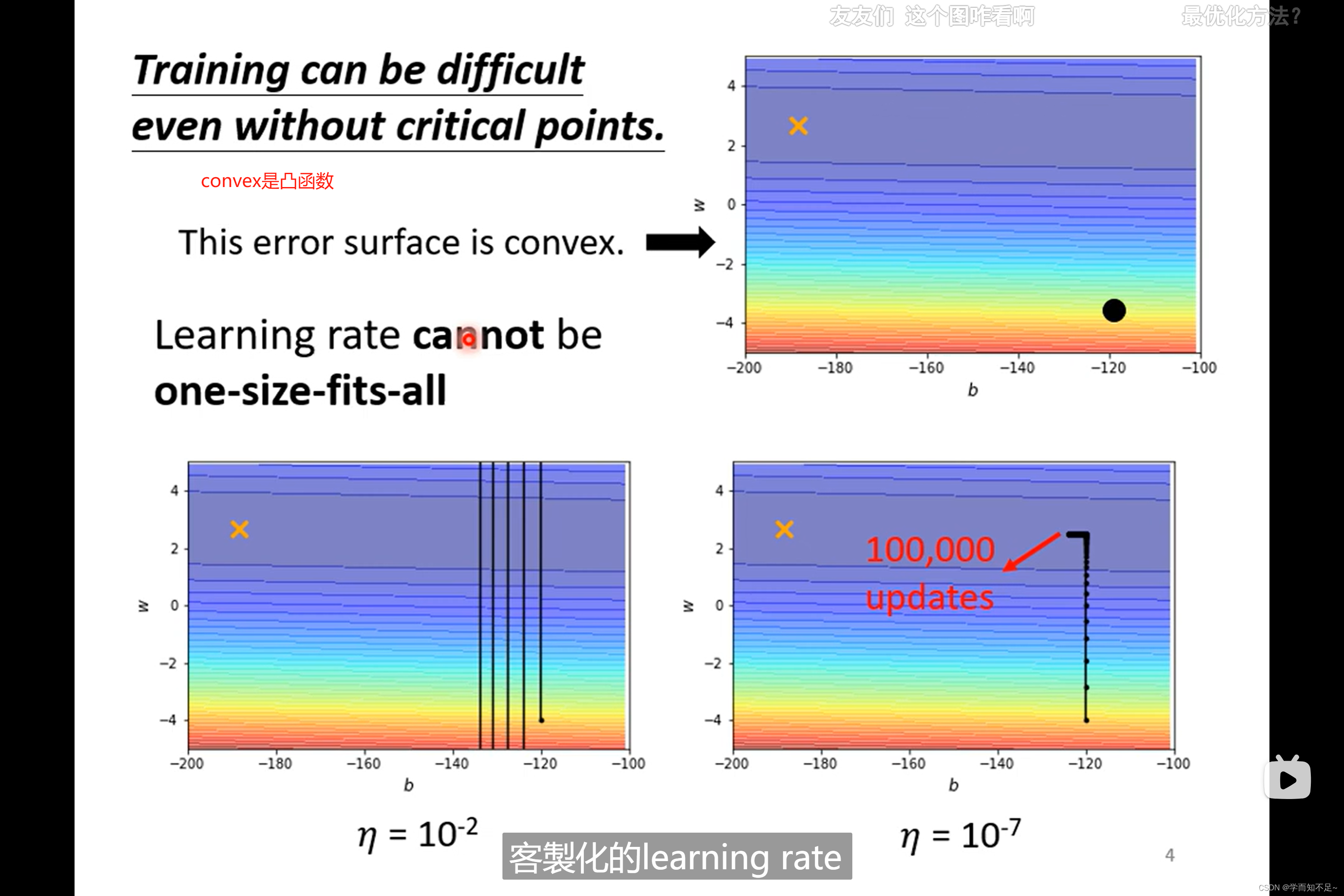
使用客制化的learning rate
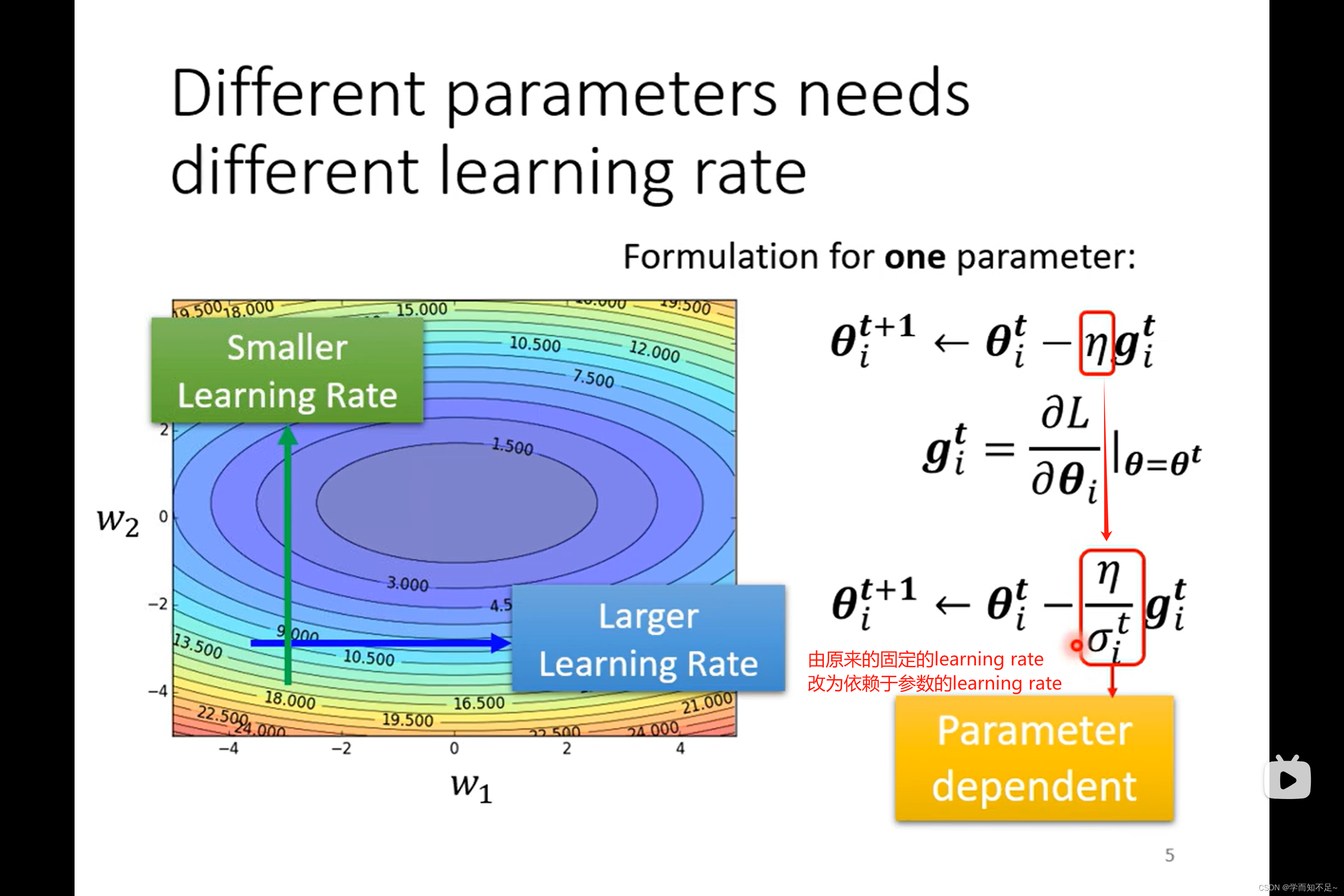
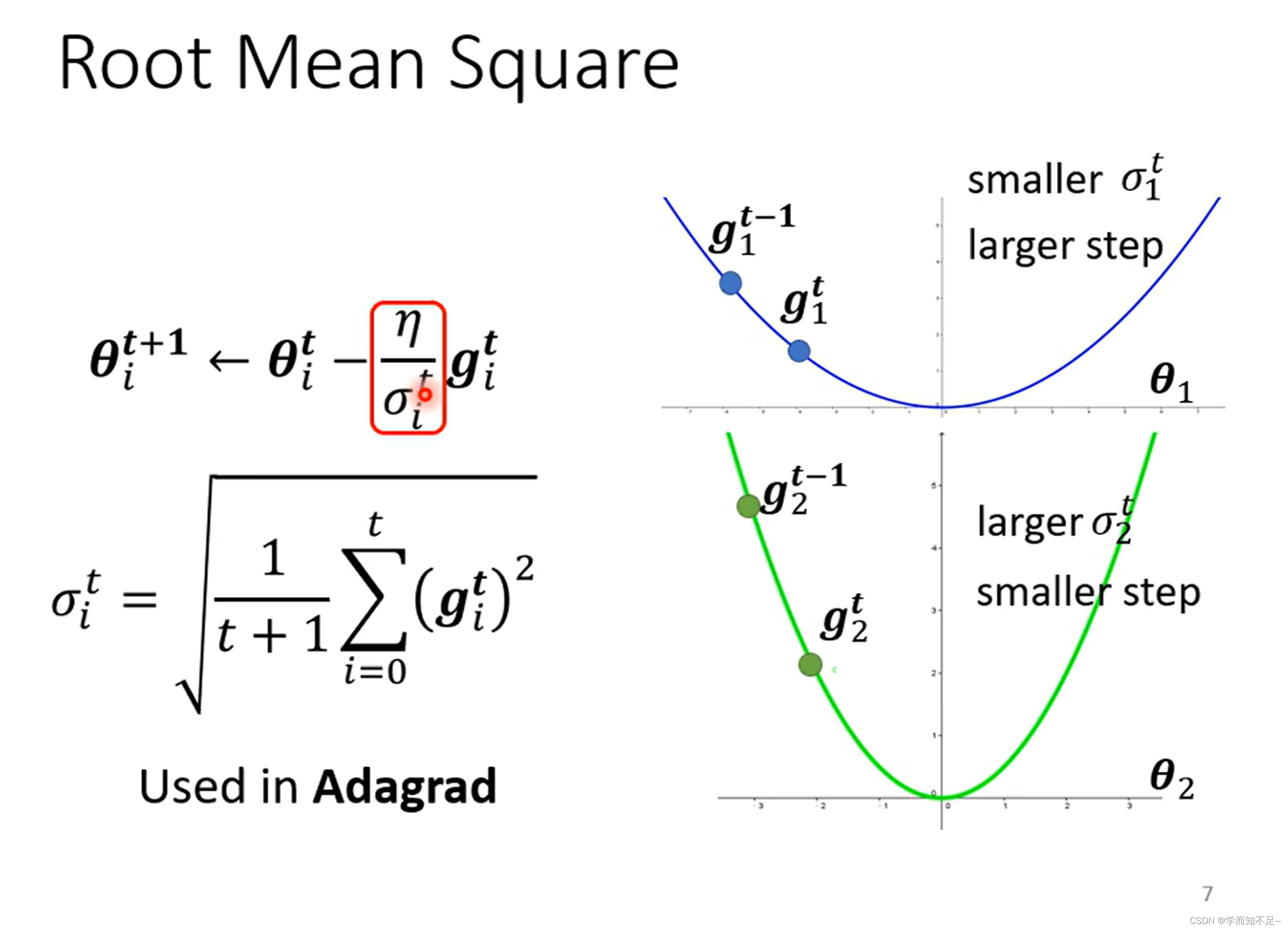
Root mean square(均方根)

这个方法被用于Adagrad算法上
当gradient变化比较平缓的时候,算出来的learning rate会更大,当gradient变化比较着急时,算出来的learning rate会比较小
存在的问题
同个参数,同个方向,均方根算出来的值是固定不变的,但是我们希望的是能够动态调整

RMSProp
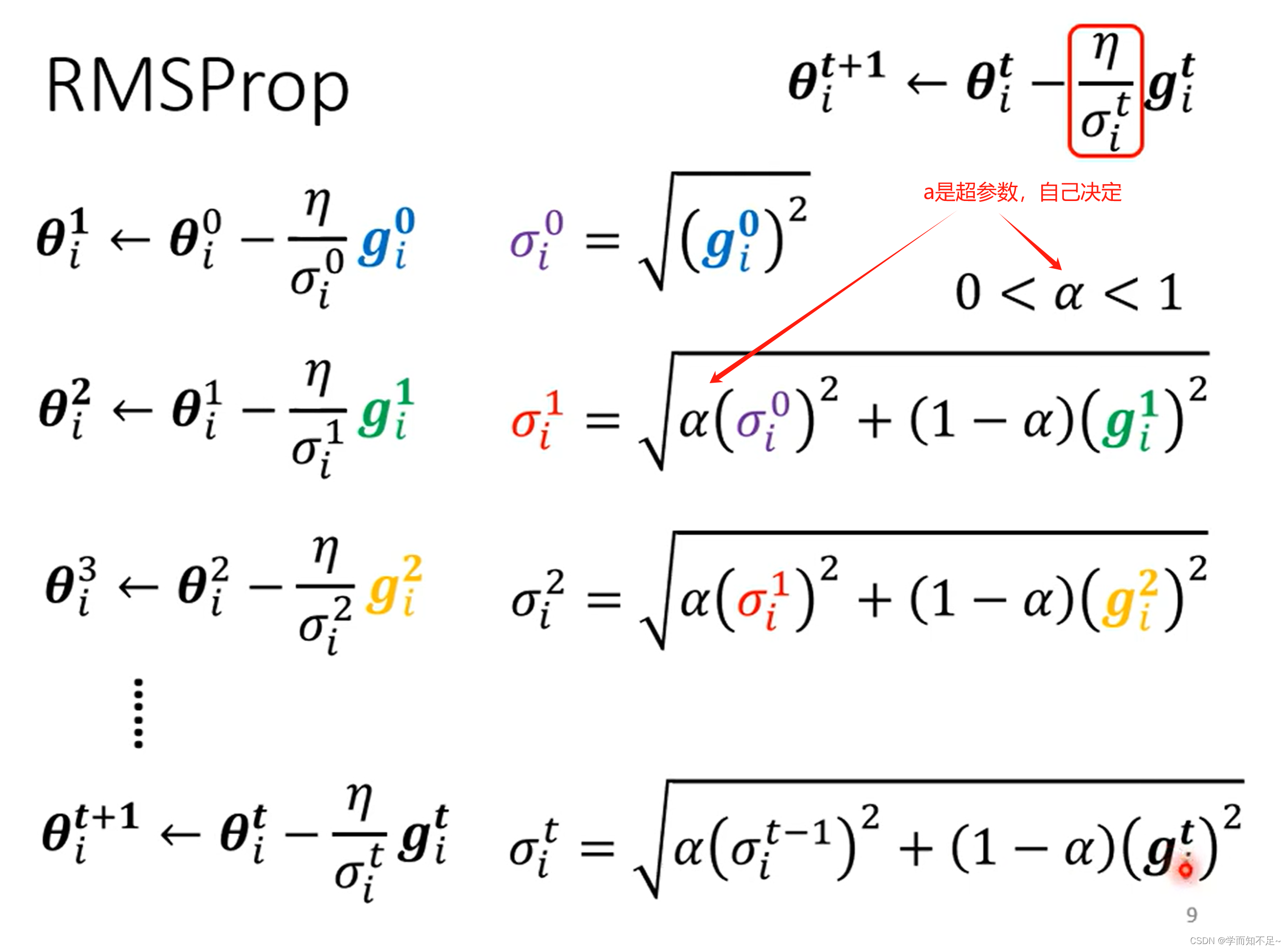
开始时比较平缓,所以算出来的learning rate很大,对应走的步伐就很大;然后当坡度变陡,则通过调整a,从而使步伐变小;当坡度变缓后,通过调整a,使得步伐又变大
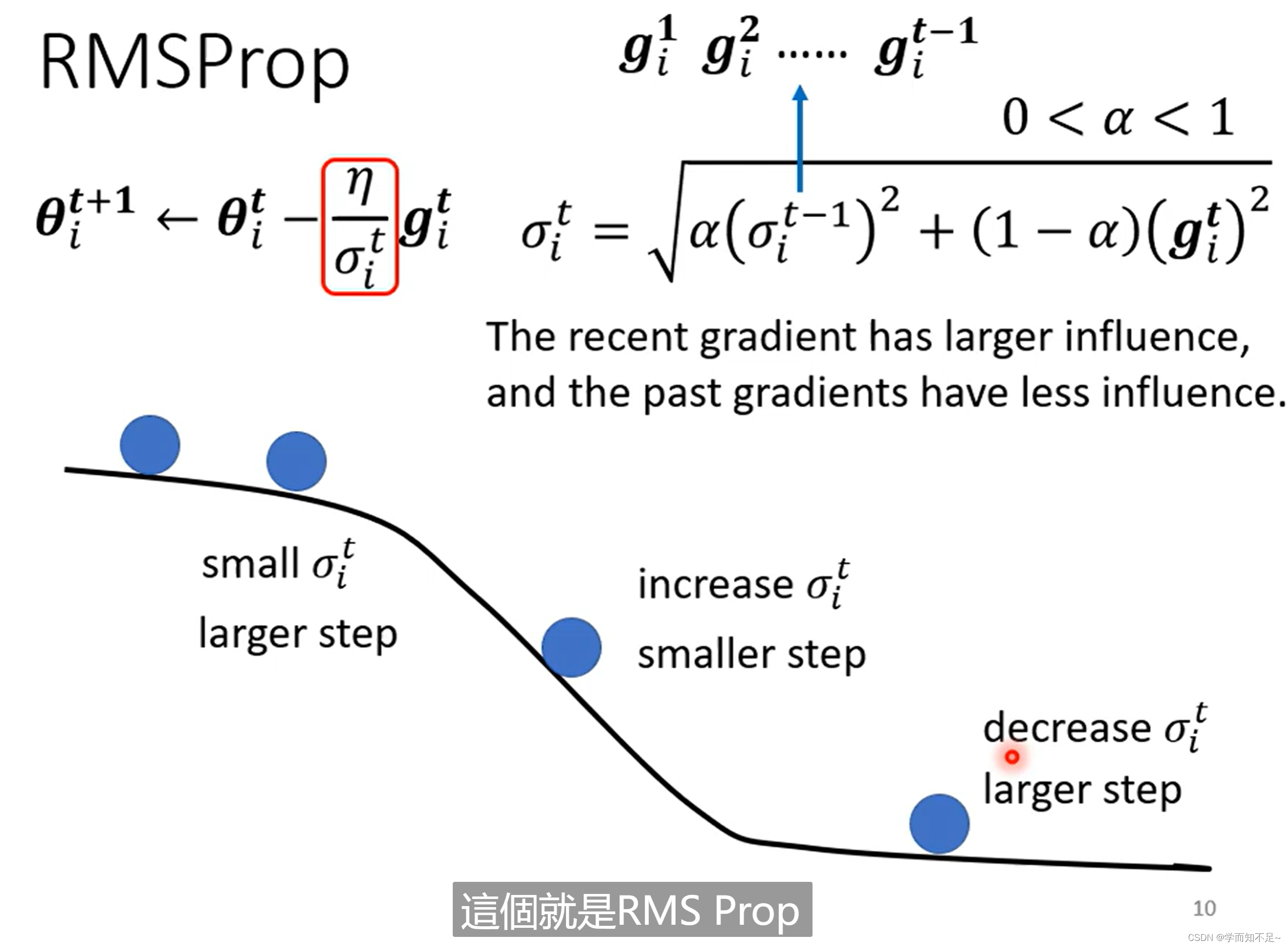
常用的Optimization策略
Adam:RMSProp + Momentum

解决开头提出的问题:无法达到最小Loss
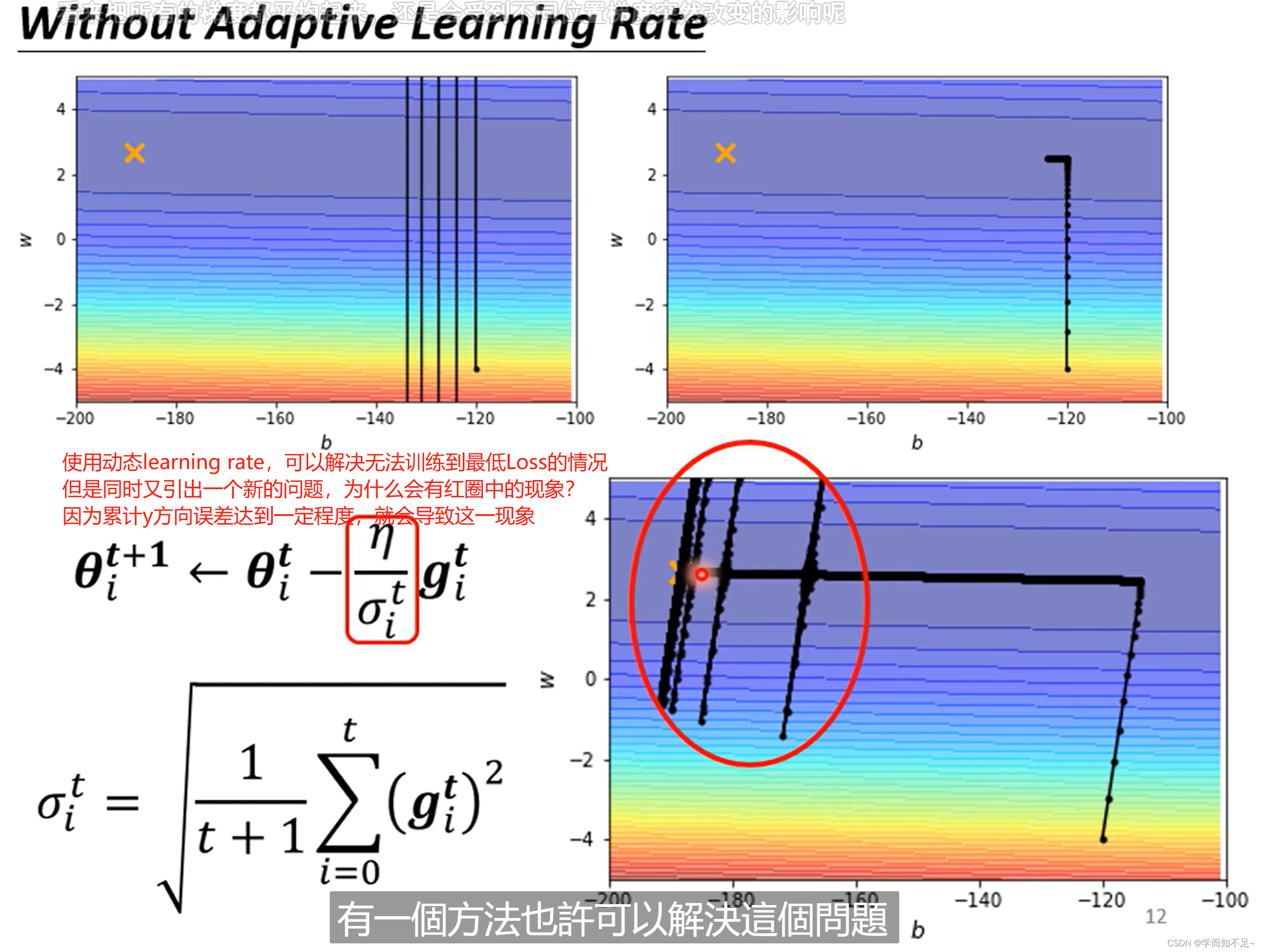
Learning Rate Scheduling
解决上述突然喷射的问题的一种方式叫Learning rate scheduling
常见的Learning rate scheduling有Learning Decay和Warm up
其中Learning Decay指的是随着时间的推移,逐渐减小n,使得Learning rate也逐渐减小,类似于踩刹车
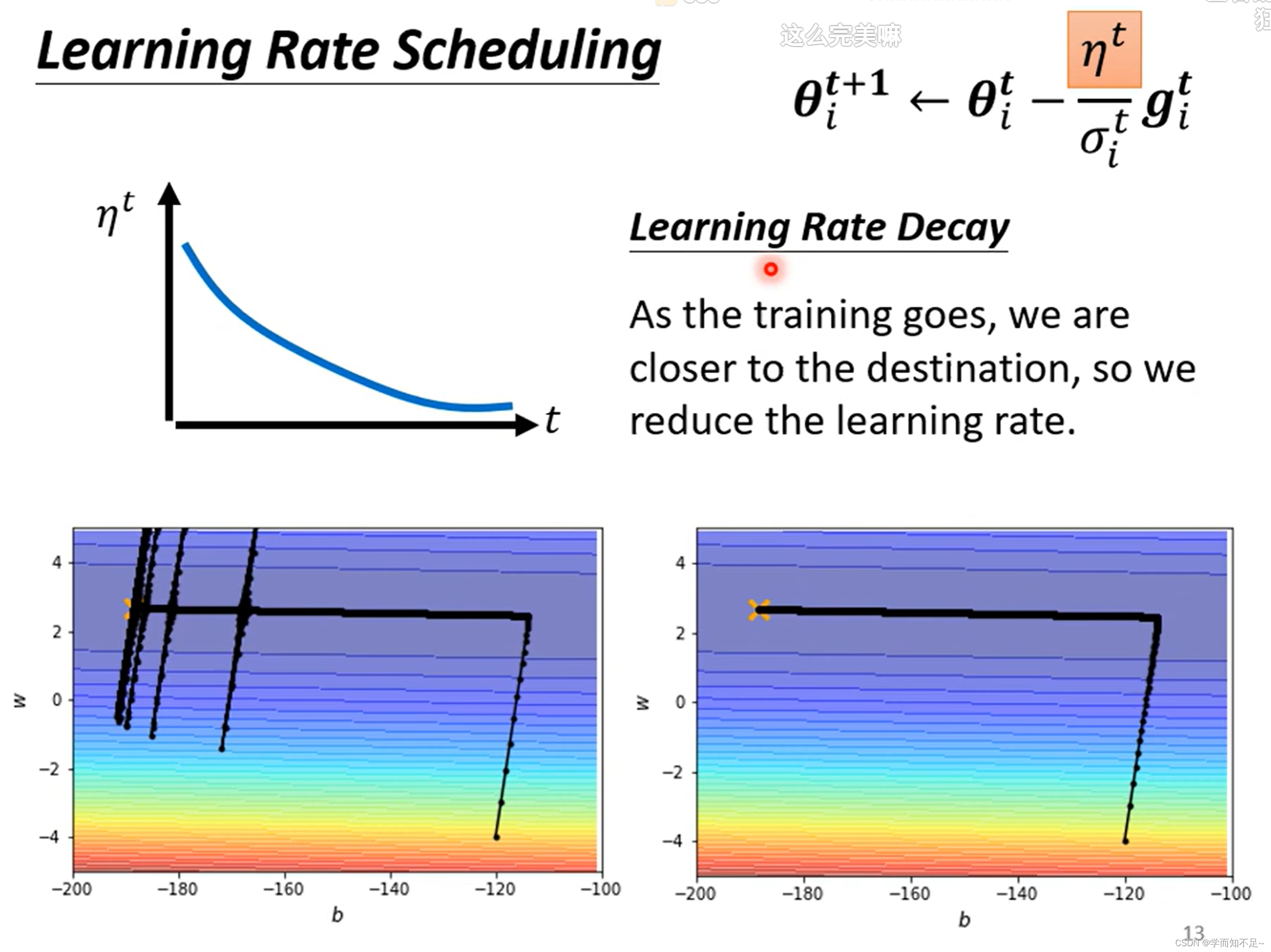
另一种方式Warm up则是指通过修改n先提高Learning rate的速度,再减小,类似于先加速再减速
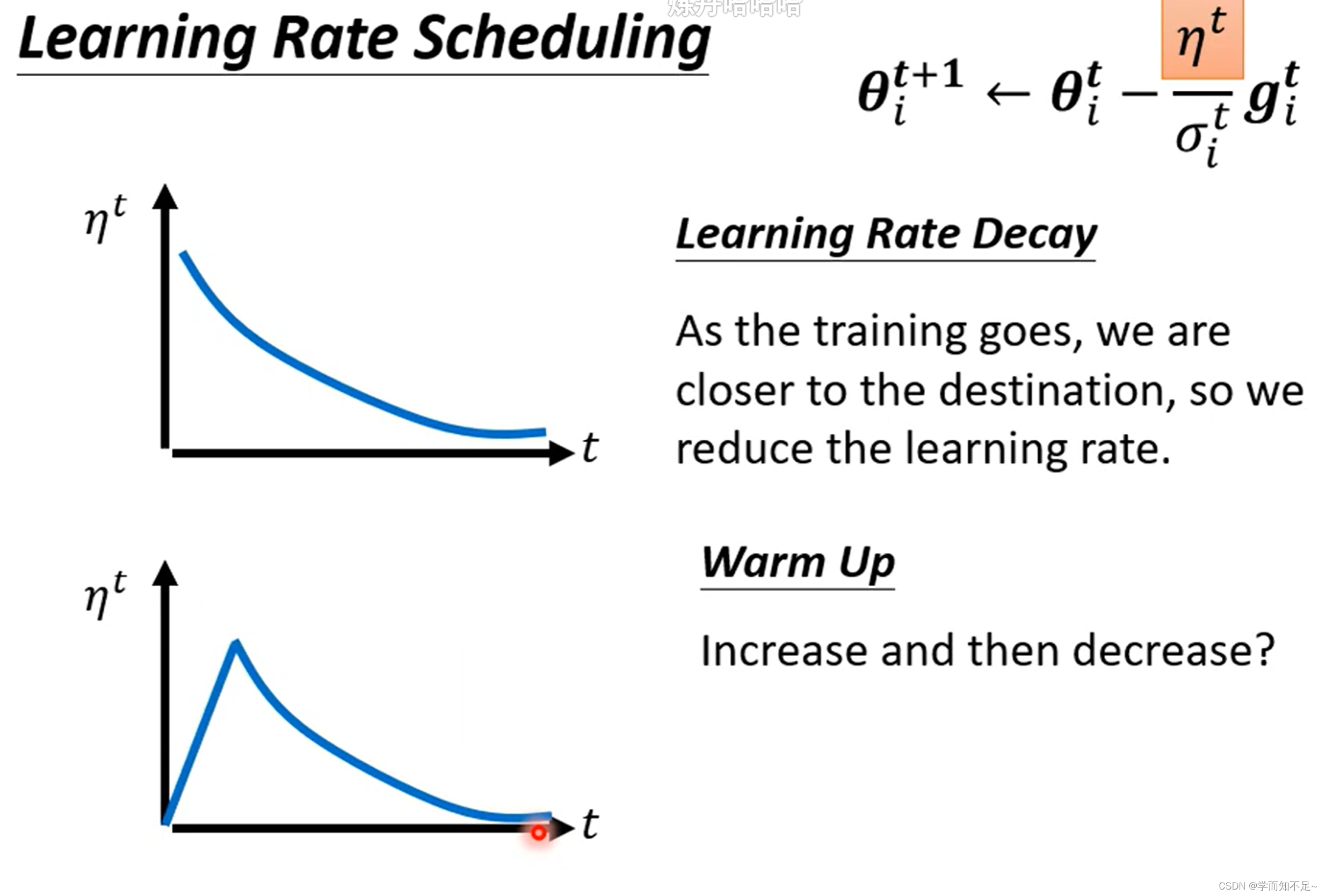
Warm up是一个黑科技,很多论文都有用到

总结

损失函数Loss对Optimization也有影响
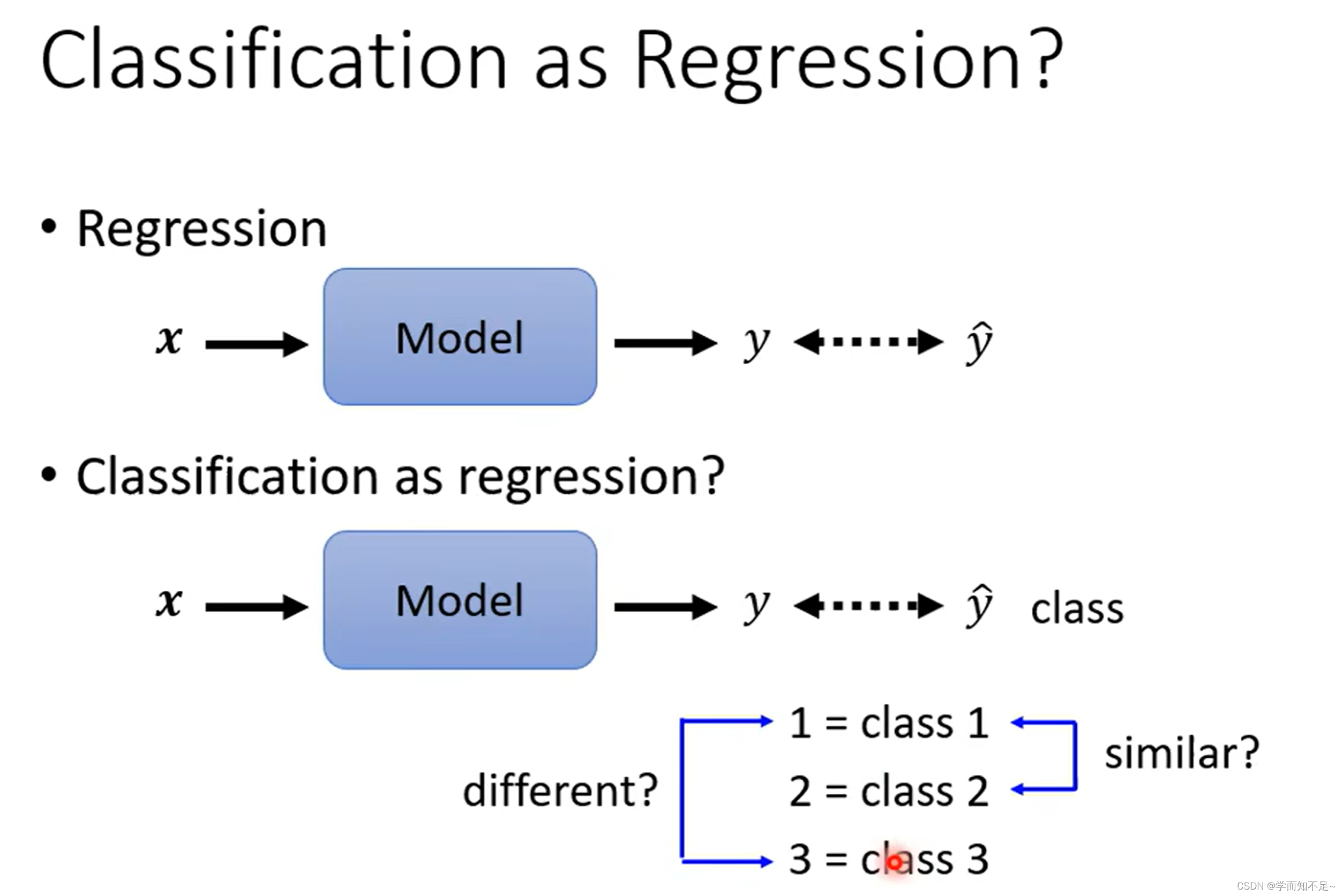
假设将分类问题按照回归问题来做
即假设class对应着数字1,2,3,
有时候可行,有时候不可行。
比如假设根据身高体重预测是几年级,由于年级之间有联系,所以可行
但是如果这几个class之间没有联系,则不可行
one-hot vector
为了解决class之间没有联系的问题,我们可以使用one-hot vector
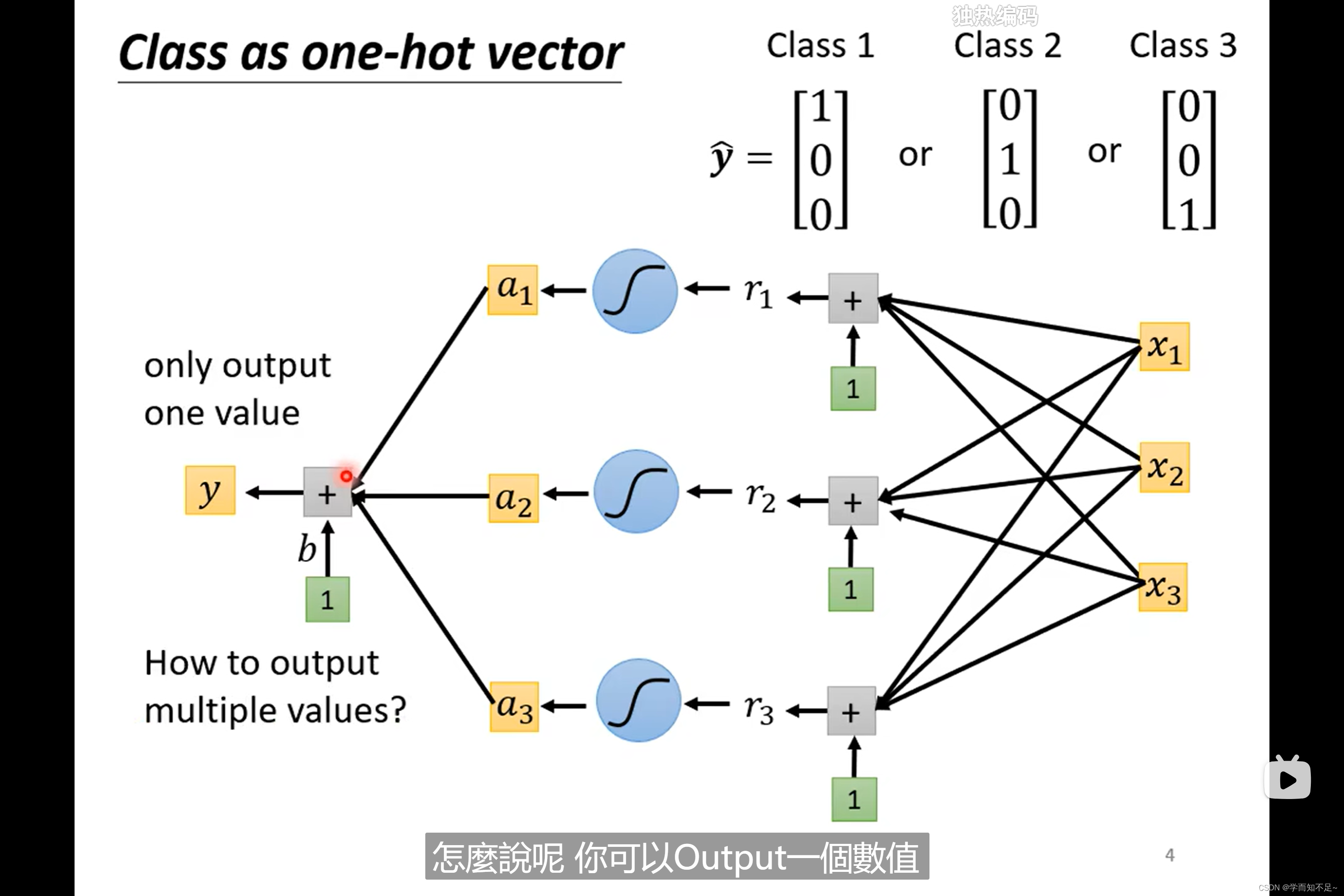
由原来的一个value推广至多个value
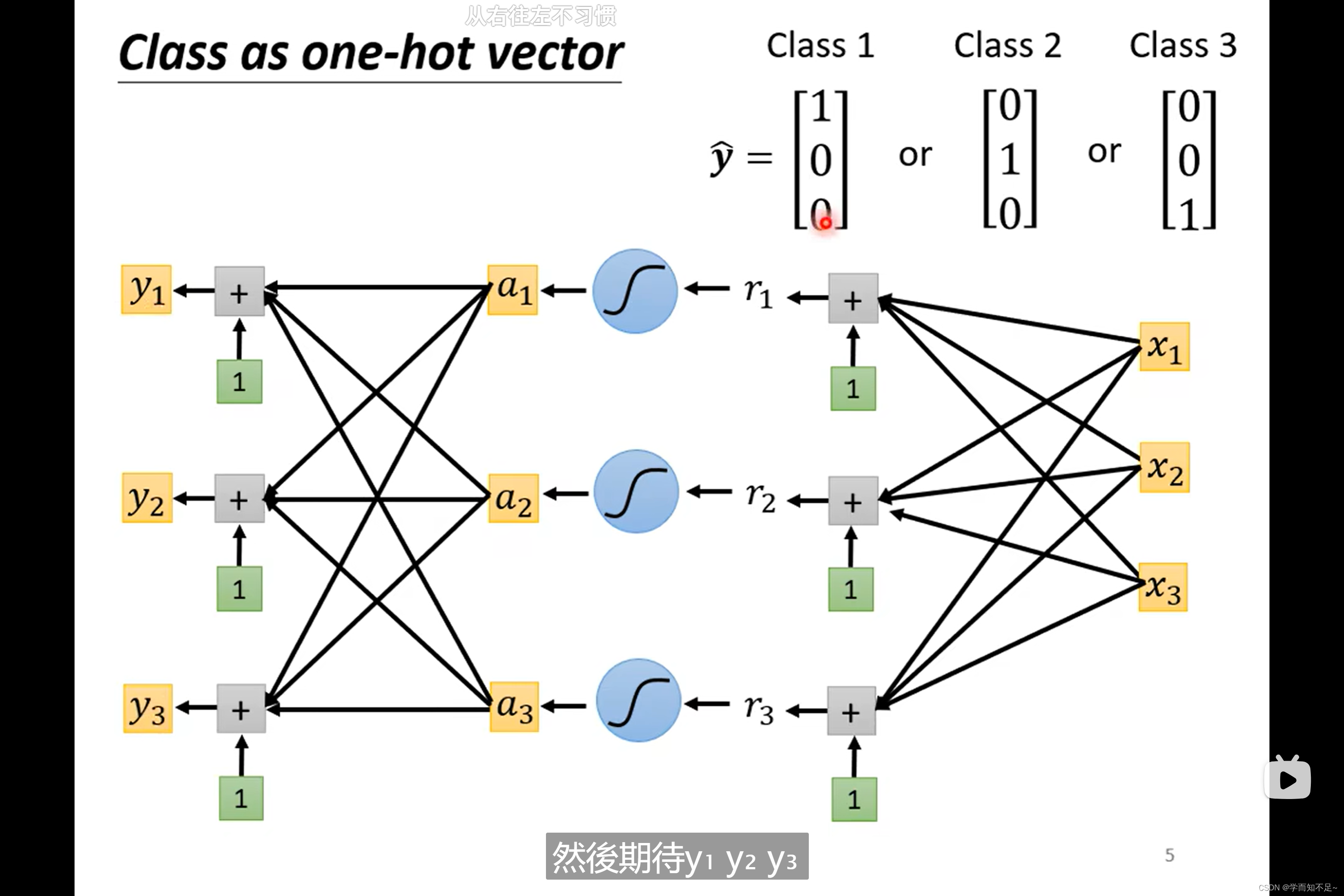
softmax(归一化)


上述是多个class的情况,如果是2个class,一般直接使用sigmoid,但是实际上这两个是等价的
Loss of classfication(分类的Loss)
分类中常用的Loss方法是Cross-entropy
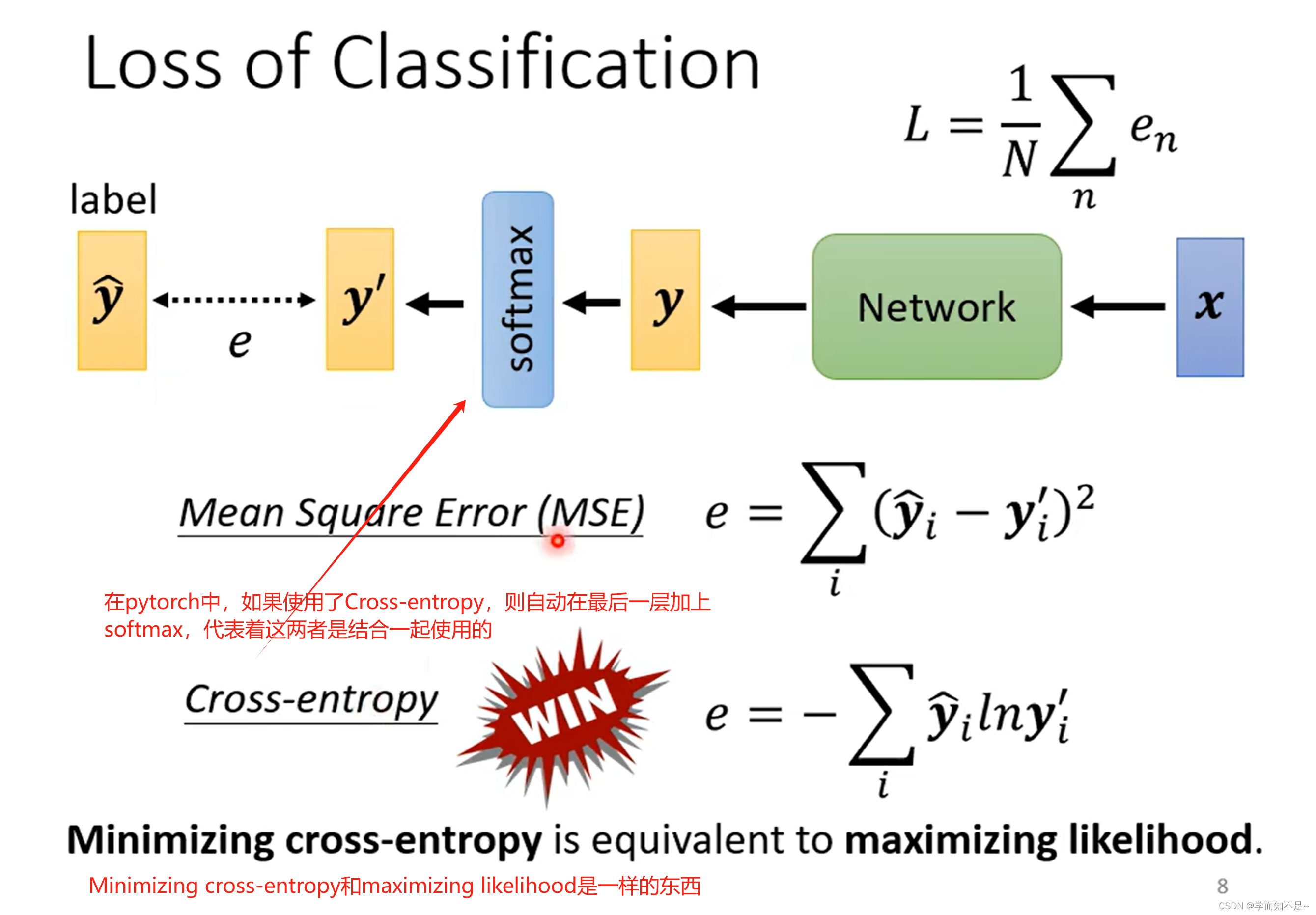
通过下面的例子我们可以看出,MSE在可能会在较大Loss的情况下卡主,而Cross-entropy则不没有问题,也侧面说明了不同的Loss定义对于优化的影响也不同
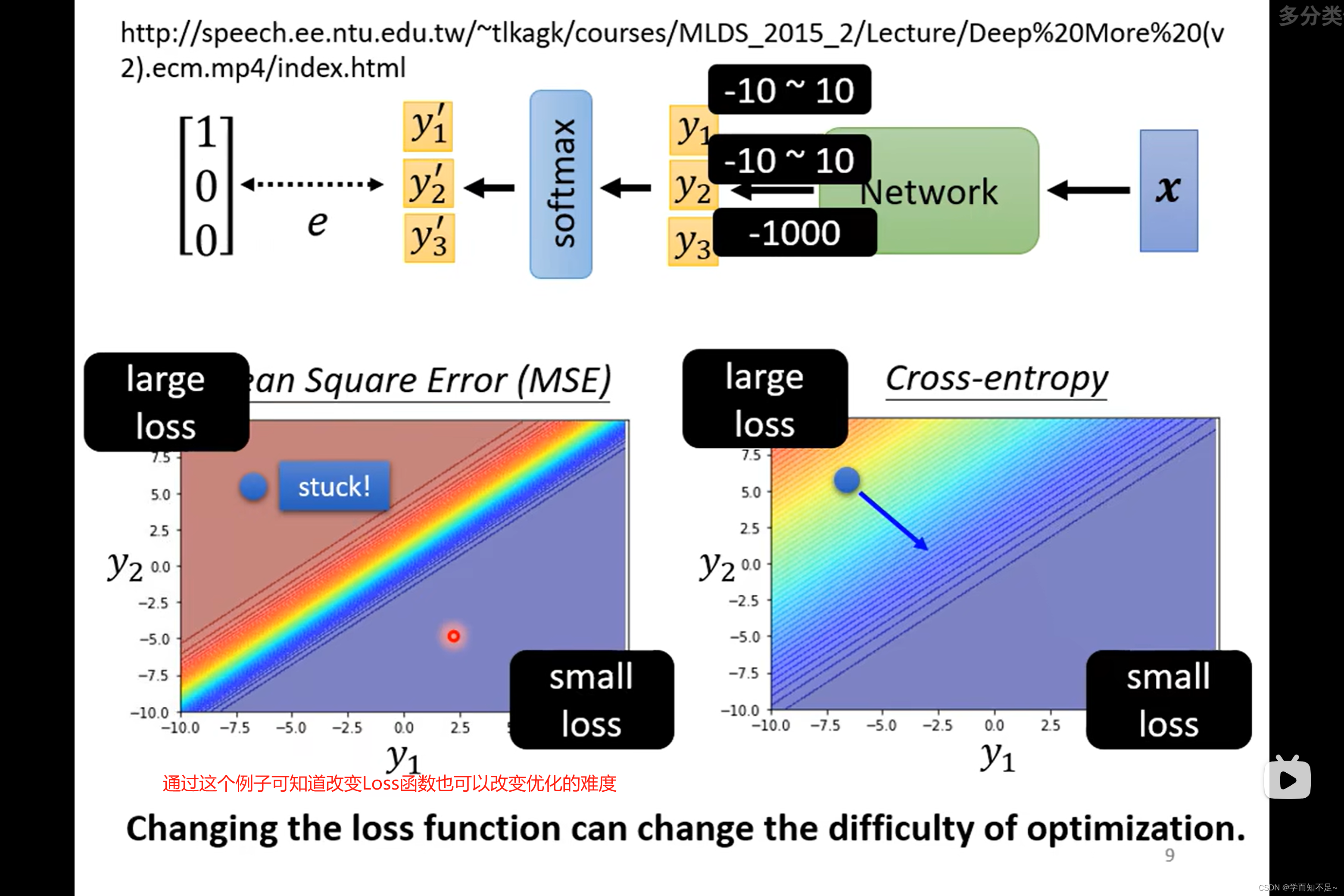
)
- 通话接听流程)

)
让工地变得更加“聪明”)




 安装lua + 卸载软件)









