2024年第九届数维杯大学生数学建模挑战赛题目
B 题 生物质和煤共热解问题的研究
(1)基于附件一,请分析正己烷不溶物(INS)对热解产率(主要
考虑焦油产率、水产率、焦渣产率)是否产生显著影响?并利用图像 加以解释。
我们可以首先计算各样品的平均焦油产率、水产率和焦渣产率,然后对比含有和不含有INS的样品之间的差异。我们将焦油产率、水产率和焦渣产率的平均值绘制成柱状图,以图像的形式展示正己烷不溶物对这些产率的影响。
首先,我们需要计算各样品的焦油产率、水产率和焦渣产率。在附件一中,每个样品有多个试验数据,我们需要计算每个样品的平均值。
然后,我们可以比较含有和不含有INS的样品的平均值,并绘制成柱状图,以展示正己烷不溶物对热解产率的影响。
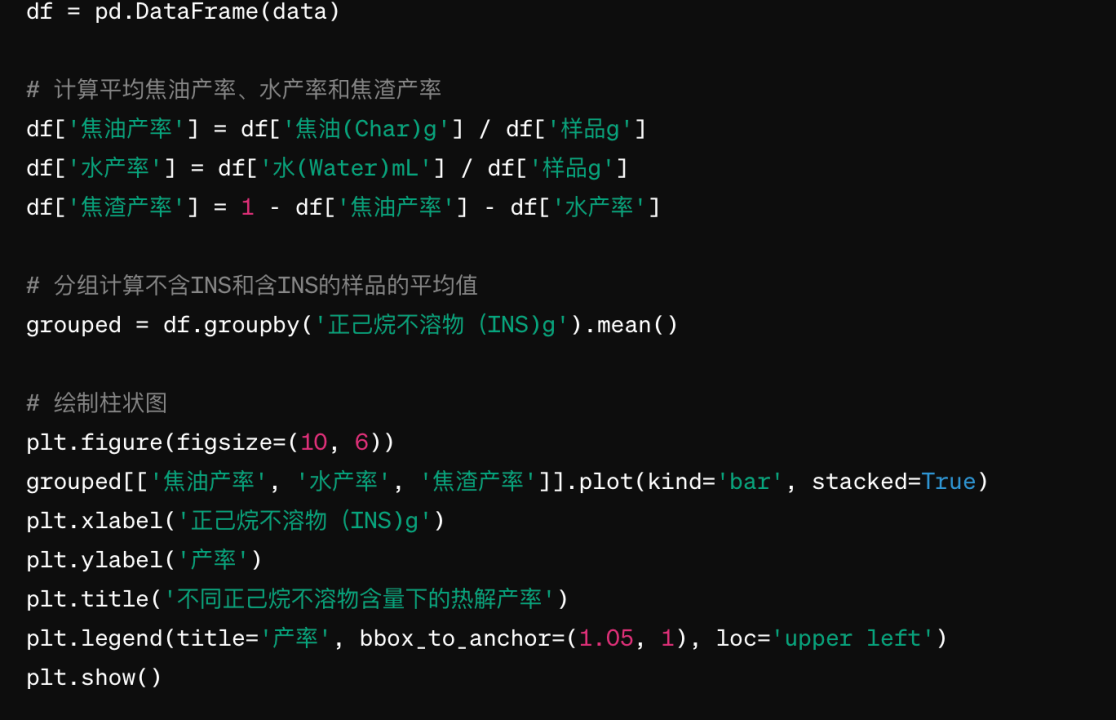
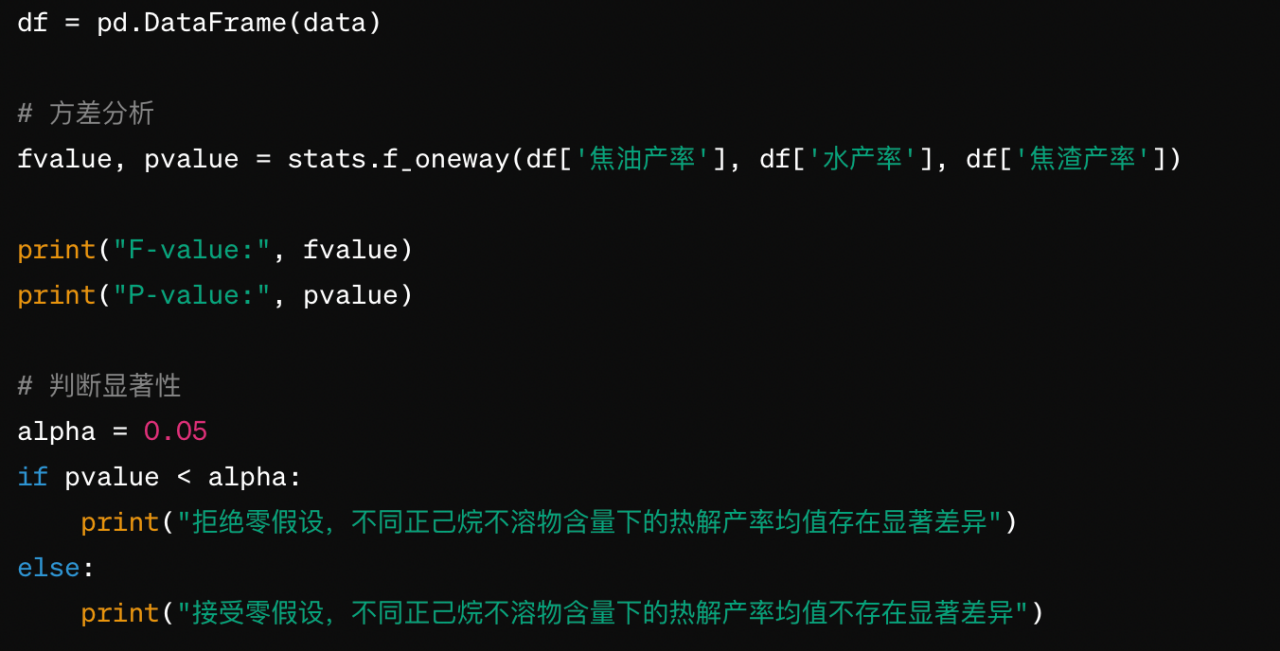
要体现正己烷不溶物(INS)对热解产率的显著影响,可以使用统计学中的假设检验方法。常见的假设检验方法包括 t 检验和方差分析(ANOVA)。在这种情况下,我们可以使用方差分析来比较不同正己烷不溶物含量下的热解产率是否存在显著差异。
具体步骤如下:
提出假设:
零假设(H0):不同正己烷不溶物含量下的热解产率均值相等。
备择假设(H1):不同正己烷不溶物含量下的热解产率均值不全相等。
进行方差分析:
计算组间平方和(SSB)和组内平方和(SSW)。
计算均方(MSB 和 MSW)。
计算 F 统计量:F = MSB / MSW。
判断显著性:
根据自由度和显著水平查找 F 分布表,找到临界 F 值。
如果计算得到的 F 统计量大于临界 F 值,则拒绝零假设,认为不同正己烷不溶物含量下的热解产率均值存在显著差异。
在进行方差分析之前,需要对数据进行一些前提检验,如正态性检验和方差齐性检验,以确保方差分析结果的可靠性。
(2)热解实验中,正己烷不溶物(INS)和混合比例是否存在交互
效应,对热解产物产量产生重要影响?若存在交互效应,在哪些具体
的热解产物上样品重量和混合比例的交互效应最为明显?
要分析正己烷不溶物(INS)和混合比例是否存在交互效应,可以使用二因素方差分析(Two-way ANOVA)来进行。二因素方差分析可以同时考虑两个因素(正己烷不溶物和混合比例)及其交互效应对因变量(热解产物产量)的影响。
具体步骤如下:
提出假设:
零假设(H0):正己烷不溶物、混合比例以及它们的交互效应对热解产物产量没有显著影响。
备择假设(H1):正己烷不溶物、混合比例或它们的交互效应对热解产物产量有显著影响。
进行二因素方差分析:
计算组间平方和(SSB1、SSB2、SSB12)和组内平方和(SSW)。
计算均方(MSB1、MSB2、MSB12、MSW)。
计算 F 统计量:F1 = MSB1 / MSW,F2 = MSB2 / MSW,F12 = MSB12 / MSW。
判断显著性:
根据自由度和显著水平查找 F 分布表,找到临界 F 值。
如果计算得到的 F 统计量大于临界 F 值,则拒绝零假设,认为正己烷不溶物、混合比例或它们的交互效应对热解产物产量有显著影响。
在具体分析交互效应的时候,可以通过检查交互作用的 P 值来确定哪些交互效应是显著的。如果交互作用显著,可以进一步分析各水平组合下的热解产物产量,以确定哪些组合对产量影响最为明显。
(3)根据附件一,基于共热解产物的特性和组成,请建立模型
优化共解热混合比例,以提高产物利用率和能源转化效率
要建立模型优化共热解混合比例,以提高产物利用率和能源转化效率,首先需要确定一个目标函数,该函数应考虑热解产物的利用率和能源转化效率。一种可能的目标函数是最大化焦油产率和水产率的总和,同时最小化焦渣产率。同时,也可以考虑最大化正己烷可溶物产率作为另一个目标。
然后,可以使用数学优化方法,如线性规划、非线性规划或进化算法等,来求解最优的混合比例。在这个过程中,需要考虑混合比例的约束条件,如混合比例之和为100等。
具体步骤如下:
确定目标函数:
目标函数1:最大化焦油产率和水产率的总和,同时最小化焦渣产率。
、目标函数1=焦油产率+水产率−焦渣产率目标函数1=焦油产率+水产率−焦渣产率
目标函数2:最大化正己烷可溶物产率。
目标函数2=正己烷可溶物产率目标函数2=正己烷可溶物产率
确定约束条件:
混合比例之和为100。
使用数学优化方法求解最优混合比例。
(4)根据附件二,请分析每种共热解组合的产物收率实验值与
理论计算值是否存在显著性差异?若存在差异,请通过对不同共热解
组合的数据进行子组分析,确定实验值与理论计算值之间的差异在哪
些混合比例上体现?
要分析每种共热解组合的产物收率实验值与理论计算值是否存在显著性差异,可以使用假设检验方法,比如 t 检验。首先,对每种组合进行 t 检验,检验实验值与理论计算值之间的差异是否显著。然后,可以对不同混合比例进行子组分析,确定实验值与理论计算值之间的差异在哪些混合比例上体现。
具体步骤如下:
对每种共热解组合进行 t 检验:
假设零假设(H0):实验值与理论计算值之间的差异不显著。
假设备择假设(H1):实验值与理论计算值之间的差异显著。
对于显著的组合,进行子组分析:
对每个混合比例进行 t 检验,检验实验值与理论计算值之间的差异是否显著。
(5)基于实验数据,请建立相应的模型,对热解产物产率进行
预测
要建立对热解产物产率进行预测的模型,可以使用回归分析。回归分析可以帮助我们理解自变量(例如混合比例)与因变量(例如焦油产率、水产率、焦渣产率等)之间的关系,并用于预测因变量的取值。
具体步骤如下:
确定因变量和自变量:
因变量:焦油产率、水产率、焦渣产率等。
自变量:混合比例等。
收集和整理实验数据,构建数据集。
选择合适的回归模型:
线性回归:假设因变量和自变量之间存在线性关系。
多项式回归:假设因变量和自变量之间存在高阶关系。
其他回归模型:根据数据特点选择适当的回归模型。
拟合回归模型:
使用数据拟合回归模型,得到模型参数。
模型评估:
分析模型的拟合程度,评估模型的准确性和可靠性。
进行预测:
使用建立的回归模型对新数据进行预测,得到热解产物的产率预测值。
)

)

逆变器simulink仿真模型)










JSP教程——exception对象)



