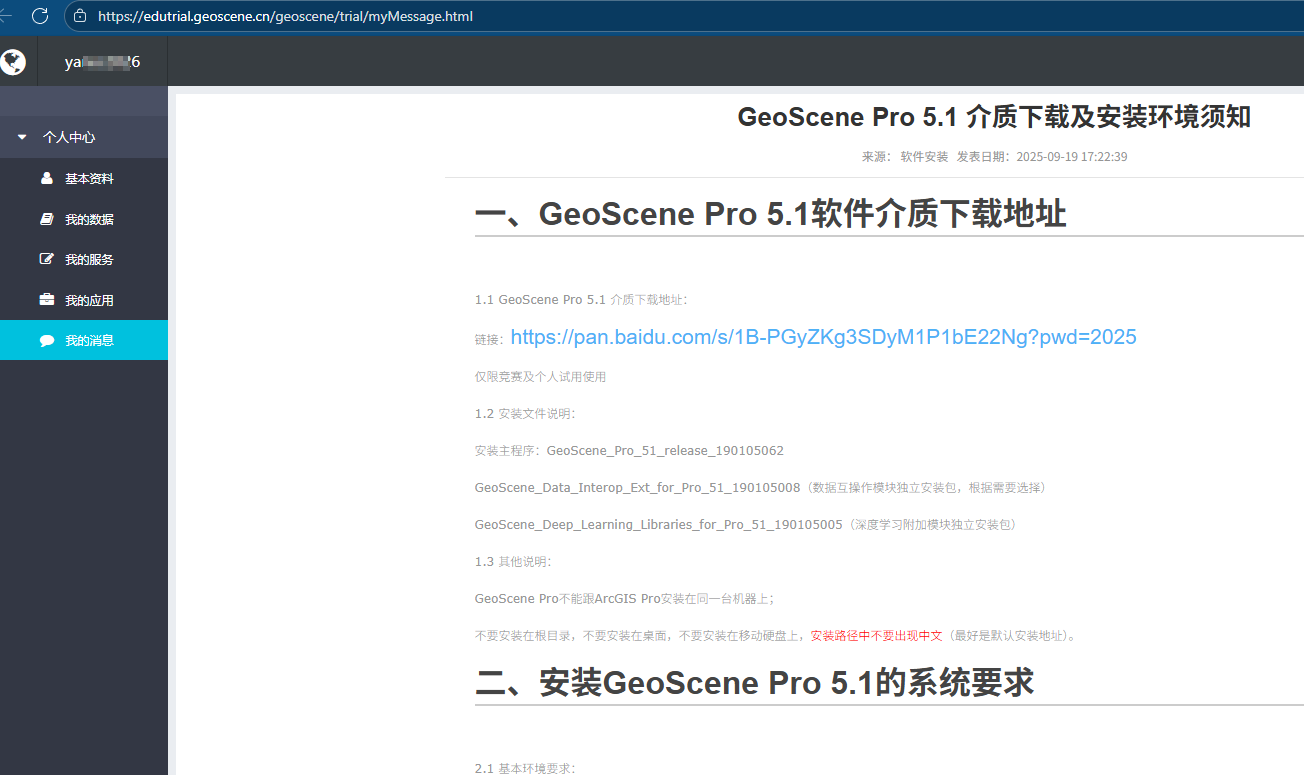
按在线的文档配置
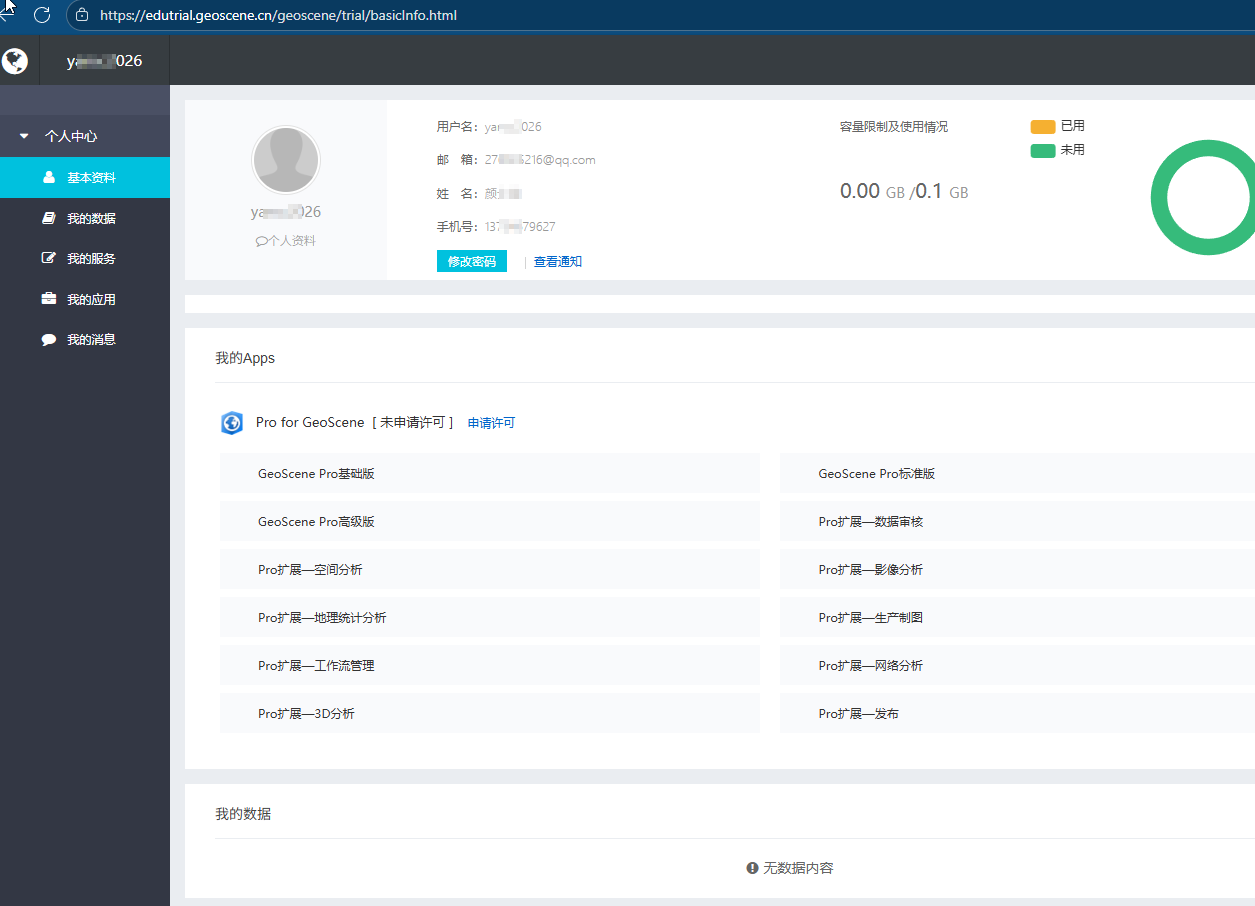
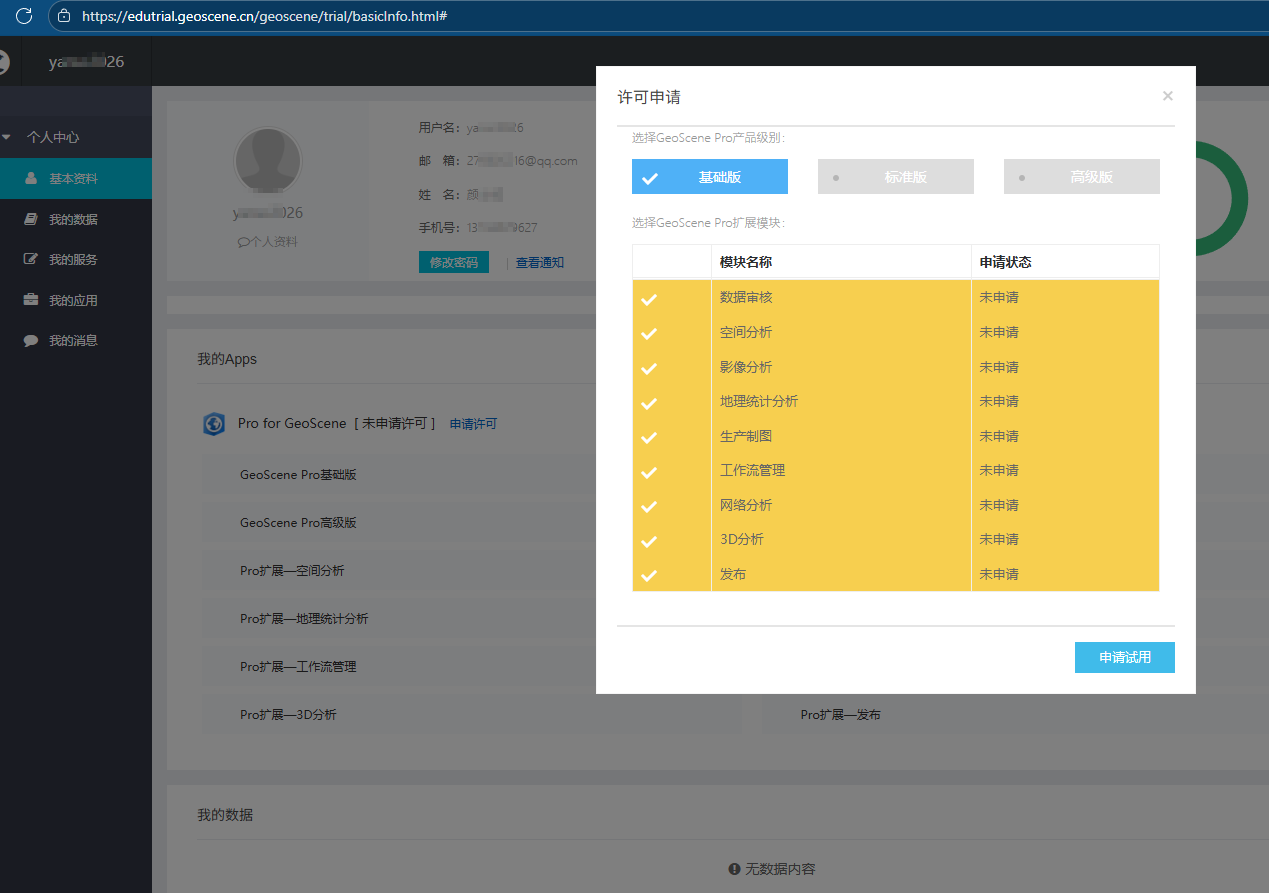
GeoScene Pro申请试用 - 易智瑞教育网
1）要求你输入许可的，如下图，这时候需要更换【许可类型】为“指定用户许可”（4.0版本软件这里写的是“授权用户许可”）
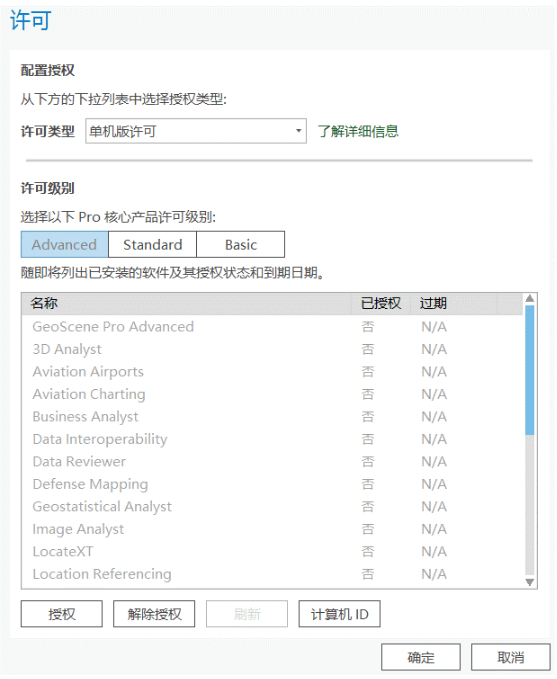
更换许可类型后，在GeoScene Enterprise那里面写（如下图）：https://edutrial.geoscene.cn/geoscene/
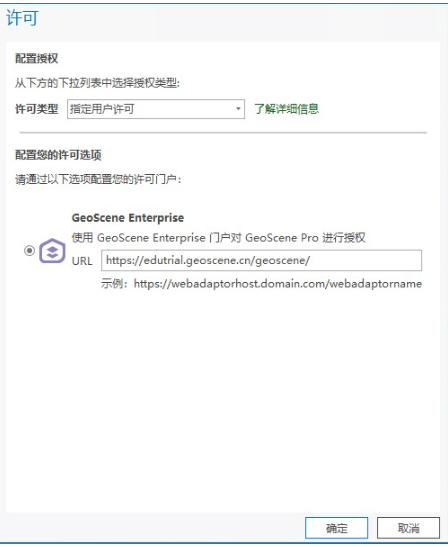
2）如果是第一次打开就直接是登录界面，点击最下方绿色的“配置许可”就可以到上面的操作，需要提醒大家，软件默认的许可服务器配置地址是GeoSceneOnline，但是实际上我们的许可服务器不是这个，留意看下图，点击左下角绿色小字“配置许可”
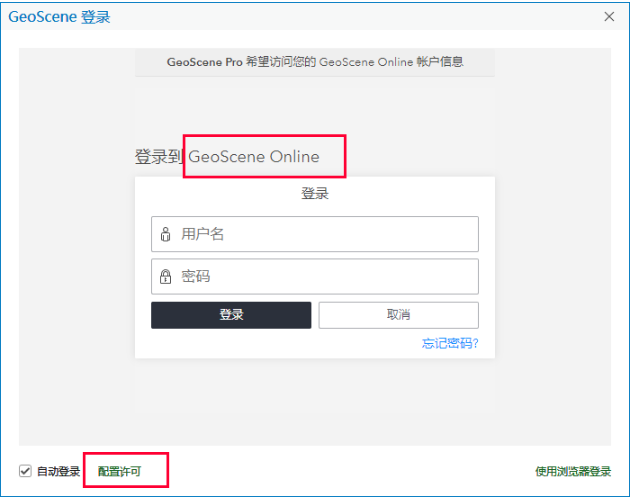
指定用户许可模式下默认登录界面
将许可服务器地址按照上面内容，写成正确的服务器地址：https://edutrial.geoscene.cn/geoscene/
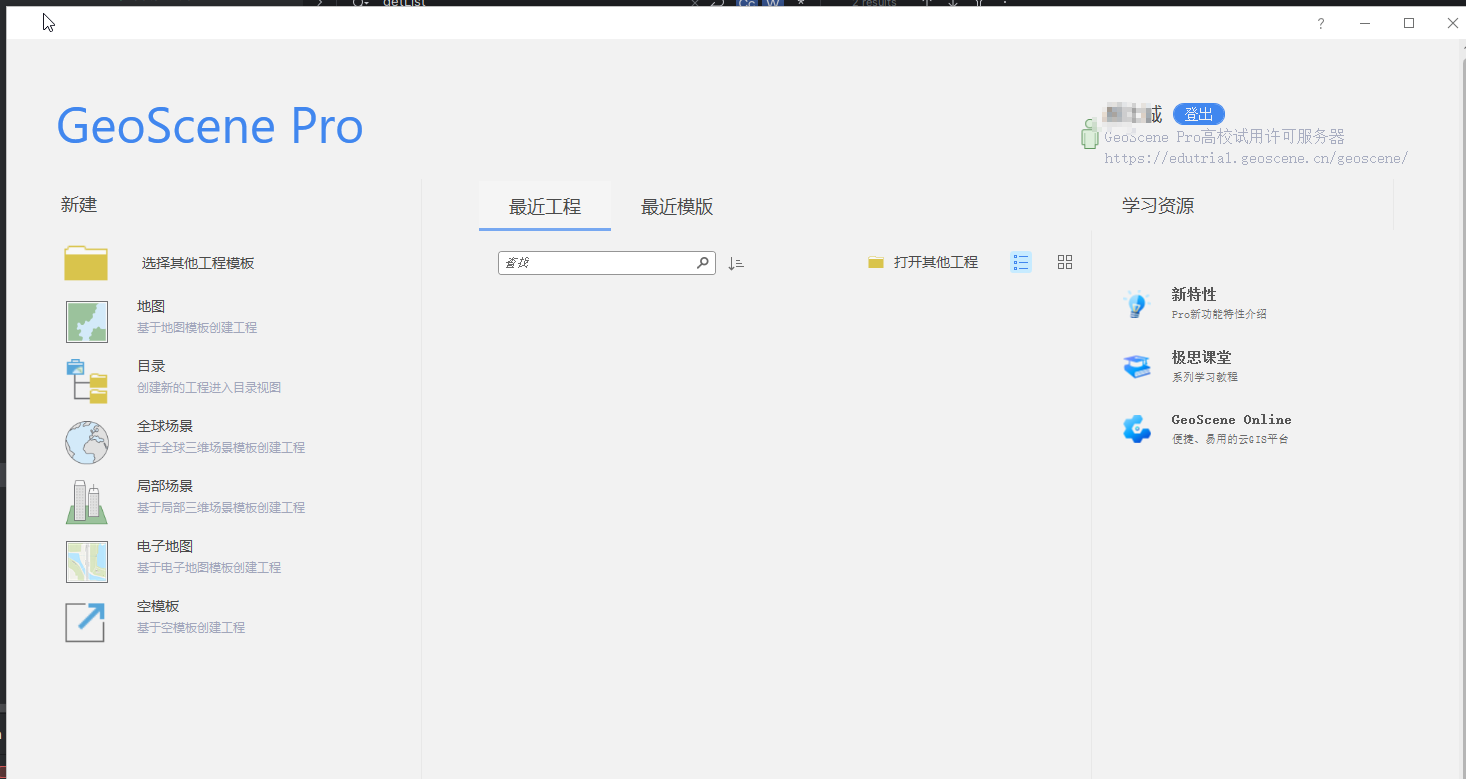
回到登录页面，输入用户名、密码，登录软件。
安装vs2022扩展
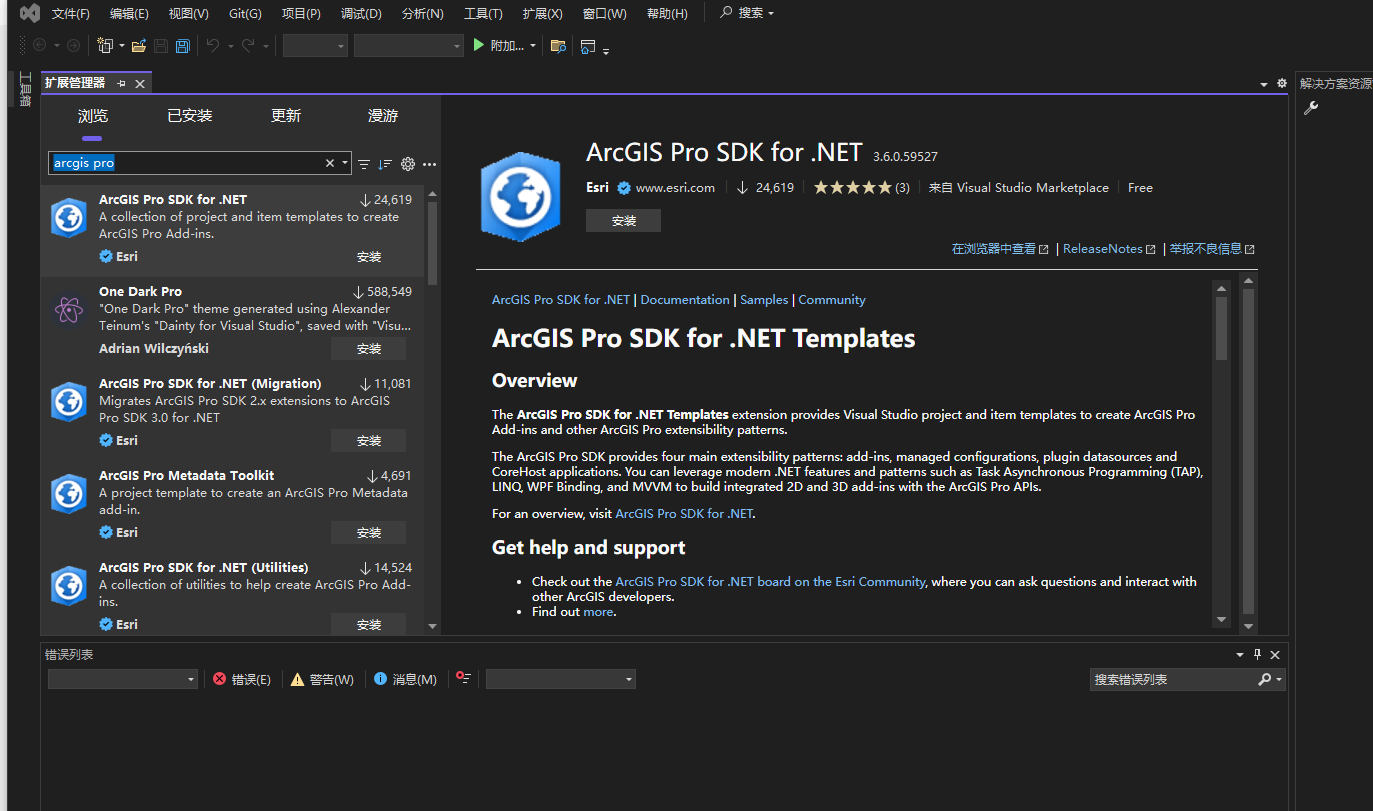
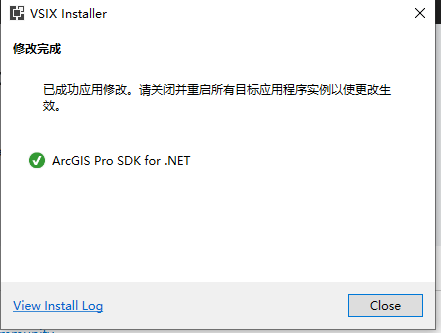
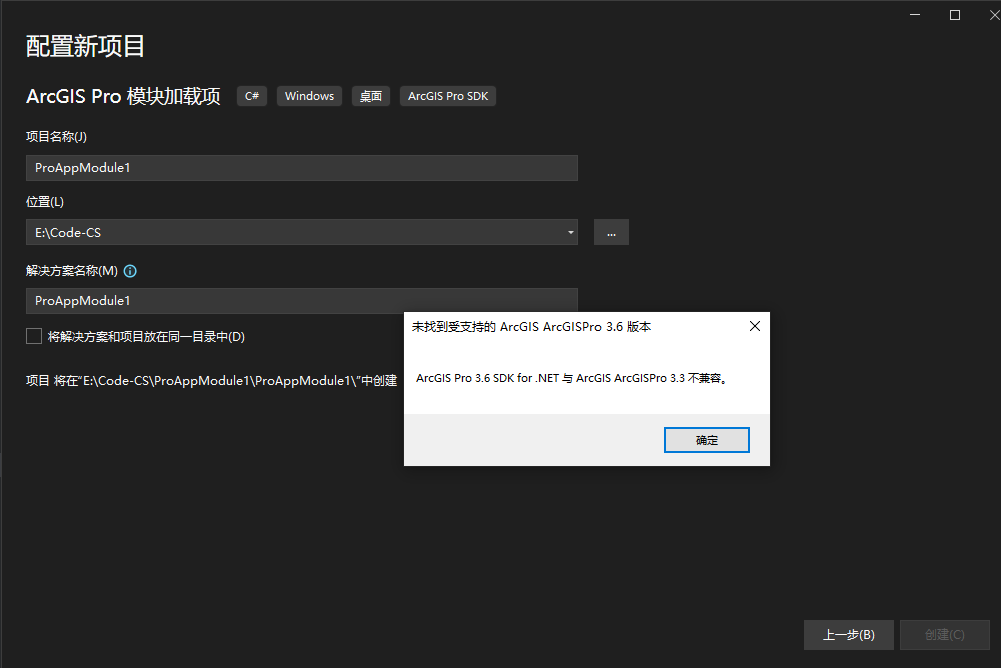
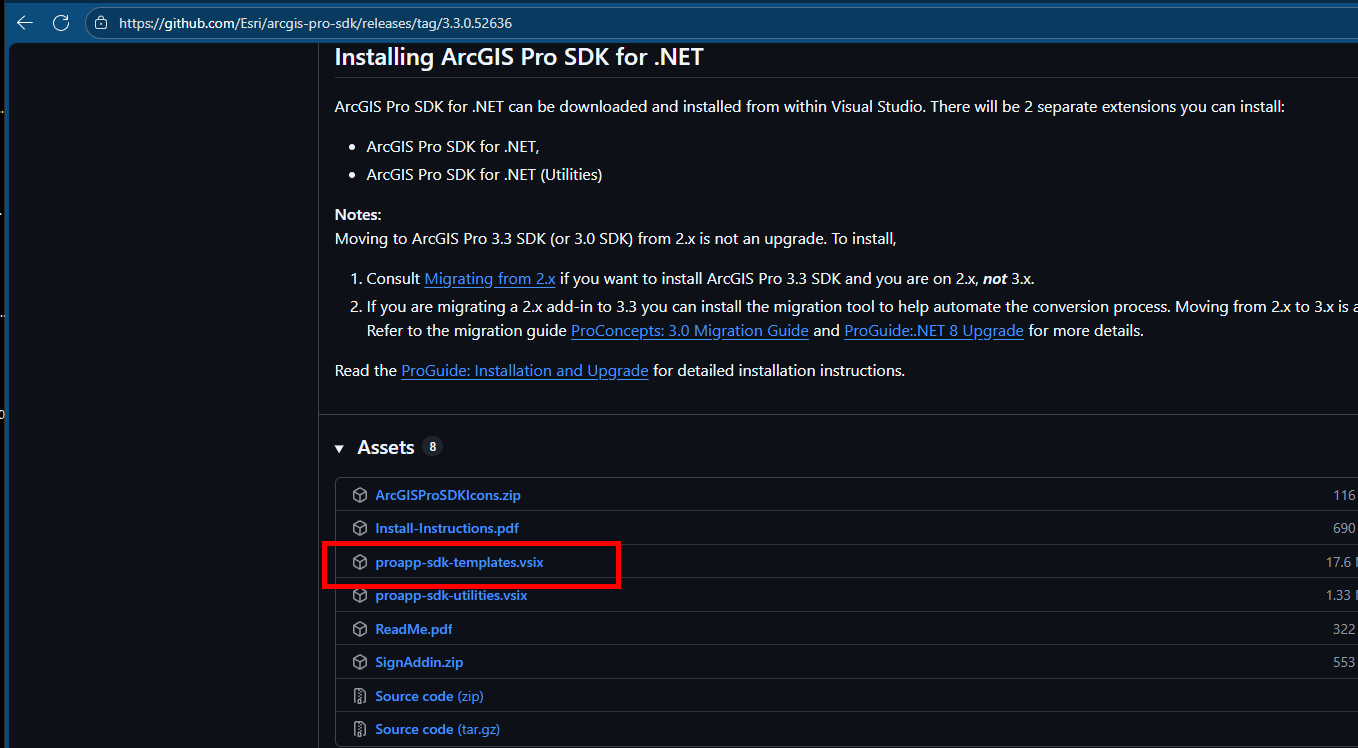
换 3.3
Release ArcGIS Pro 3.3 SDK for .NET · Esri/arcgis-pro-sdk · GitHub
Releases · Esri/arcgis-pro-sdk-community-samples · GitHub
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/965711.shtml
如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
![题解：P13573 [CCPC 2024 重庆站] Pico Park](http://pic.xiahunao.cn/题解：P13573 [CCPC 2024 重庆站] Pico Park)
题解：P13573 [CCPC 2024 重庆站] Pico Park
P13573：区间 DP、组合数学VP 的时候没题可跟了，就开了这题切掉了，结果 VP 结束发现正赛就一个队伍过了？？？
若 \(x\) 用缩小枪击中了 \(y\)，则从 \(x\) 向 \(y\) 连一条有向边。注意到，任何一个时刻得到的图是若…
【AI智能体】Coze 提取对标账号短视频生成视频文案实战详解 - 指南
pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", …
Java Benchmark使用
如何测量Java代码的性能
在 Java 中，可以使用多种方法来测量一段代码的执行性能。使用 System.currentTimeMillis()是最常见的方法
long startTime = System.currentTimeMillis();// 需要测量的代码块
for (int i = 0…
实用指南：12-机器学习与大模型开发数学教程-第1章1-4 导数与几何意义
pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", …
基于Vue社区共享游泳馆预约高效的系统n897q36e （工具+源码+数据库+调试部署+开发环境）带论文文档1万字以上，文末可获取，系统界面在最后面。
pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", …
docker登录容器镜像仓库
容器镜像仓库就是我们平时自己构建的镜像有一个存储的位置，方便自己平时进行拉取，测试用的我使用的是ucloud这容器仓库ucloud.cn登录容器仓库的操作docker logindocker login uhub.service.ucloud.cn# username 为登…
吴恩达深度学习课程二： 改善深层神经网络 第三周：超参数调整，批量标准化和编程框架（一）超参数调整
此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下：原课程视频链接：[双语字幕]吴恩达深度学习deeplearning.ai
github课程资料，含课件与笔记:吴恩达深度学习教学资料
课程配套练习（中英）与答案…
Kotlin中的flow、stateflow、shareflow之间的区别和各自的功能 - 教程
Kotlin中的flow、stateflow、shareflow之间的区别和各自的功能 - 教程2025-11-14 20:36
tlnshuju
阅读(0)
评论(0) 收藏
举报pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto…
![非离散网络流——P3347 [ZJOI2015] 醉熏熏的幻想乡](http://pic.xiahunao.cn/非离散网络流——P3347 [ZJOI2015] 醉熏熏的幻想乡)
非离散网络流——P3347 [ZJOI2015] 醉熏熏的幻想乡
非离散网络流——P3347 [ZJOI2015] 醉熏熏的幻想乡
观察费用为 \(a_ix^2+b_ix\)，如果是离散的，则可以套路的建边 \(a_i+b_i,3a_i+b_i,5a_i+b_i,\dots\)，可本题 \(x\in R\)。
于是连续意义下我们应该求导得到 \(2a_i…
![[note] 素数判定与分解质因数](http://pic.xiahunao.cn/[note] 素数判定与分解质因数)
[note] 素数判定与分解质因数
在某些毒瘤的数论题中，可能出现对 \(10^{18}\) 的范围内的数质因数分解的情况。这时，可以使用 Fermat 和 Miller-Rabin 算法进行素性判定，Pollard-Rho 算法寻找非平凡因子，两者结合以快速质因数分解。
Fermat 素性…
不能识别adb/usb口记录 - 实践
pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", …
恭喜自己，挑战成功！ - Ghost
恭喜自己，挑战成功！
我终于，拿省一啦！
正文：
在2025年8月18日，本人开始了一项挑战
挑战三个月达省一
在三个月后，2025年11月14日，NOI官网发布了分数and分数线
本人以高出一等分数线10分的分数（250pts），成功…
如何在测试覆盖不足后补充验证
测试覆盖不足是项目质量的重大隐患，一旦发现（尤其是当它已导致线上问题时），团队必须立即采取系统性的补充验证措施。核心策略是停止盲目开发，转而执行一套以风险为导向的补救流程。 首先，必须立即对未覆盖的区域…
完整教程：PDFBox - PDDocument 与 byte 数组、PDF 加密
pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !important; display: block !important; font-family: "Consolas", "Monaco", "Courier New", …
Dark Side of the Moon
“Speak to Me”
"Ive been mad for fucking years, absolutely years, been over the edge for years, been working me buns off for bands..."
"Ive always been mad, I know Ive been mad, like mo…
flask:自定义异常
一，代码：
自定义异常:class ApiError(Exception):""""API接口异常错误"""messsage = ""# 默认错误码status_code = 400# 自定义一个return_code, 作为更细粒的错误代码…
