2025-11-14 ZYZ28-NOIP模拟赛-Round6 hetao1733837的record

比赛链接：ZYZ28-NOIP模拟赛-Round6

比赛背景：无

A.teleport

提交链接：teleport

题面

给定一个$N$个节点（节点有对应坐标），$M$条边的带权无向联通图，此外，从点$u$到点$v$不仅可以通过边，也可以支付$\min(|x_u-x_v|,|y_u-y_v|)$来到达。问从$1$号节点出发的单源最短路。(不知道叙述的到不到位)。

分析

观察发现，强行$O(n^2)$建图是无法通过的，考虑线段树优化建图……我并不会。考场上发现对于$u(x_u,y_u)$和$v(x_v,y_v)$之间通过点之间瞬移较为优的情况是在以两者为左下角和右上角的矩形中走出一个凸包？个人感觉比较像，可能是错的，但是理解起来更好受。那么，我们只需要对于$x$和$y$分别排序，然后统计相邻节点即可（就差这一步，我好烫）。最后，跑一遍$Dijkstra$结束！

正解

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 200005;
int n, m;
struct node{int x, y, id;
}pos[N];
bool cmp1(node a, node b){return a.x < b.x;
} 
bool cmp2(node a, node b){return a.y < b.y;
}
vector<pair<int, int>> e[N];
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
int d[N];
bool vis[N];
void dijkstra(int S){for (int i = 1; i <= n; i++)d[i] = 0x3f3f3f3f3f3f3f3f;memset(vis, 0, sizeof(vis));d[S] = 0;q.push({d[S], S});while (!q.empty()){auto o = q.top();int l = o.first, u = o.second;q.pop();if (vis[u])continue;for (auto o : e[u]){int v = o.first, w = o.second;if (d[v] > d[u] + w){d[v] = d[u] + w;q.push({d[v], v});}}}
}
signed main(){freopen("teleport.in", "r", stdin);freopen("teleport.out", "w", stdout);ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m;bool flag = 1;for (int i = 1; i <= n; i++){cin >> pos[i].x >> pos[i].y;if (pos[i].x != pos[i].y)flag = 0;pos[i].id = i;}for (int i = 1; i <= m; i++){int u, v, w;cin >> u >> v >> w;e[u].push_back({v, w});e[v].push_back({u, w});}sort(pos + 1, pos + n + 1, cmp1);for (int i = 1; i < n; i++){e[pos[i].id].push_back({pos[i + 1].id, abs(pos[i].x - pos[i + 1].x)});e[pos[i + 1].id].push_back({pos[i].id, abs(pos[i].x - pos[i + 1].x)});}sort(pos + 1, pos + n + 1, cmp2);for (int i = 1; i < n; i++){e[pos[i].id].push_back({pos[i + 1].id, abs(pos[i].y - pos[i + 1].y)});e[pos[i + 1].id].push_back({pos[i].id, abs(pos[i].y - pos[i + 1].y)});}dijkstra(1);for (int i = 2; i <= n; i++)cout << d[i] << " ";
}

B.permutation

提交链接：permutation

题面

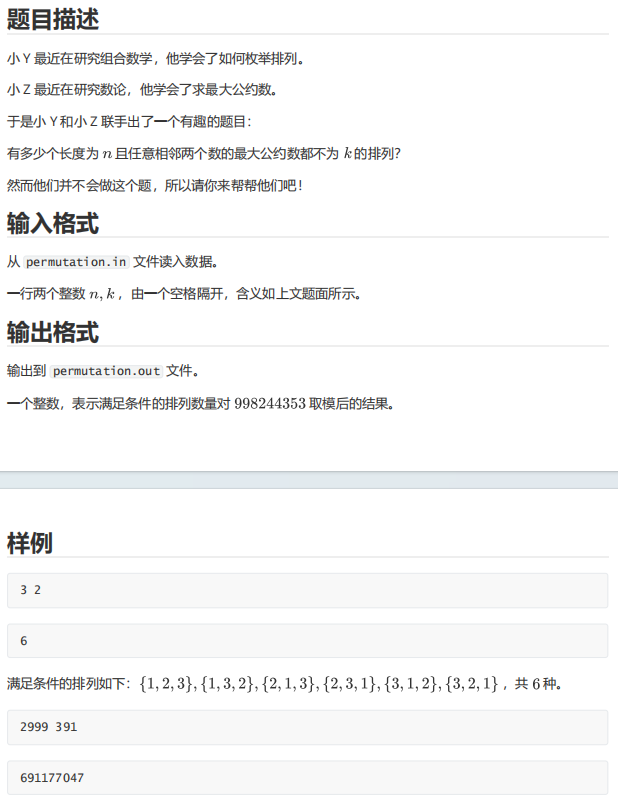
分析

显然，我们在考场上尽全力推出了式子，但是适用范围很小，正解状压$DP$我不想多说，但是，AeeE5x的组合数学令我很感兴趣，现在就去问。（14点55分）发现他在睡觉，那先研究状压$DP$。

方法一：状压$DP$

$1\le \frac{n}{k}\le10$是突破口，我也意识到了。（14点56分）他醒了。

考虑设$f_{i,j,k}$表示当前是第$i$位，这十个数的出现情况状压之后是$j$，最后一个（如果是这10个之中的）是哪一个。

转移枚举下一位放谁即可。注意对于不是关键的数字，可以认为是1，然后后期再加上这部分的方案数。

复杂度$O(n\times 2^{10}\times 11^2)$

还可以滚动数组优化，不过没必要。

方法二：组合数学+二项式定理

设存在$tmp$个$k$的倍数。

设$f_i$表示钦定$i$个数互不相邻剩余随便放，固定$n-tmp$个数，相当于插板，还有剩下的全排列，得出式子$f_i=fac_{n-tmp}\times \dbinom{n-tmp+1}{i}$。但是，并不完整，上午我们也意识到了$\gcd(2k,4k)=2k$，像这样的可以放在一起，那么，会出现诸如$f_5+2f_4+f_3$的式子，他们的系数满足杨辉三角，这样统计下来，就可以过了。

正解

方法二

#include <bits/stdc++.h>
#define int long long
#define mod 998244353
using namespace std;
const int N = 3005;
int fac[N], fac_inv[N];
int calc(int n, int m){return fac[n] * fac_inv[n - m] % mod * fac_inv[m] % mod; 
}
int qpow(int a, int b){int res = 1;while (b){if (b & 1)res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}
int n, k;
int d[25], gcd[25][25];
signed main(){freopen("permutation.in", "r", stdin);freopen("permutation.out", "w", stdout);ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> k;if (n == 1){cout << 1;return 0;}if (k == 1){cout << 0;return 0;}fac[0] = 1;for (int i = 1; i <= n; i++){fac[i] = fac[i - 1] * i % mod;}fac_inv[n] = qpow(fac[n], mod - 2);for (int i = n - 1; i >= 0; i--){fac_inv[i] = fac_inv[i + 1] * (i + 1) % mod;}int tmp = n / k;if (tmp == 1){cout << fac[n];return 0;}int ans = 0;for (int i = 1; i <= tmp; i++)for (int j = 1; j <= tmp; j++)gcd[i][j] = __gcd(i, j);for (int i = 1; i <= tmp; i++)d[i] = i;do{int cnt = 0; //打包插板 for (int i = 2; i <= tmp; i++)cnt += (gcd[d[i - 1]][d[i]] != 1);for (int i = 0; i <= cnt; i++)ans = (ans + fac[n - tmp] * calc(n - tmp + 1, tmp - i) % mod * calc(cnt, i)) % mod;}while (next_permutation(d + 1, d + 1 + tmp));cout << ans;
}

C.simulator

提交链接：simulator

题面

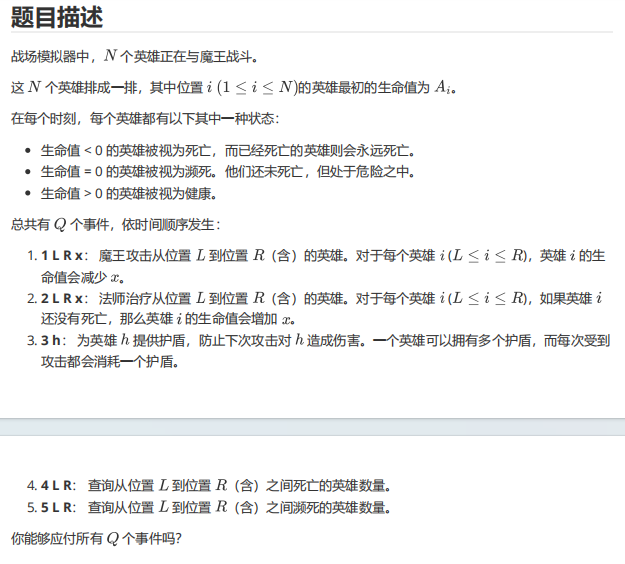
83c224cab3071a65b0b96b416a15a51d

分析

场上一眼定出神秘线段树，可是没能写出来。

使用线段树维护区间最小值，区间最小值个数，区间死亡个数，区间总护甲数。遇到护甲、die等情况，直接暴力。

正解

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INT_MAX (int)(1e18)
#define mid (l+r>>1)
const int N=2e5+10; 
int n;
int a[N],b[N];
int trd[N<<2]; //die的人 trd
int trm[N<<2]; //除去die的人最小值 trm
int trc[N<<2]; //除去die的人最小值个数 trc
int trh[N<<2]; //有护盾的人 trh
int lan[N<<2]; //血量更改懒标记 lan 
inline int read(){int t=0,f=1;register char c=getchar();while(c<'0'||c>'9') f=(c=='-')?(-1):(f),c=getchar();while(c>='0'&&c<='9') t=(t<<3)+(t<<1)+(c^48),c=getchar();return t*f;
}
void pushup(int bian){trd[bian]=trd[bian<<1]+trd[bian<<1|1];trh[bian]=trh[bian<<1]+trh[bian<<1|1];trm[bian]=min(trm[bian<<1],trm[bian<<1|1]);if(trm[bian<<1]==trm[bian<<1|1]) trc[bian]=trc[bian<<1]+trc[bian<<1|1];else if(trm[bian<<1]>trm[bian<<1|1]) trc[bian]=trc[bian<<1|1];else trc[bian]=trc[bian<<1];
}
void pushdown(int bian){trm[bian<<1]+=lan[bian],trm[bian<<1|1]+=lan[bian],lan[bian<<1]+=lan[bian],lan[bian<<1|1]+=lan[bian],lan[bian]=0;
}
void build(int bian,int l,int r){if(l==r){trd[bian]=0,trm[bian]=a[l],trc[bian]=1;return;}build(bian<<1,l,mid);build(bian<<1|1,mid+1,r);pushup(bian);
}
void update(int bian,int l,int r,int L,int R,int x){if(L<=l&&R>=r&&!trh[bian]&&trm[bian]>=x){trm[bian]-=x,lan[bian]-=x;return;}if(l==r){if(trh[bian]){trh[bian]--;return;}if(trm[bian]<x){trm[bian]=INT_MAX,trd[bian]=1,trh[bian]=0;return;}}pushdown(bian);if(L<=mid) update(bian<<1,l,mid,L,R,x);if(R>mid) update(bian<<1|1,mid+1,r,L,R,x);pushup(bian);
}
void update1(int bian,int l,int r,int L,int R,int x){if(L<=l&&R>=r){trm[bian]+=x,lan[bian]+=x;return;}pushdown(bian);if(L<=mid) update1(bian<<1,l,mid,L,R,x);if(R>mid) update1(bian<<1|1,mid+1,r,L,R,x);pushup(bian);
}
void update2(int bian,int l,int r,int x){if(l==r){if(trd[bian]!=1) trh[bian]++;return;}pushdown(bian);if(x<=mid) update2(bian<<1,l,mid,x);else update2(bian<<1|1,mid+1,r,x);pushup(bian);
}
int query(int bian,int l,int r,int L,int R){if(L<=l&&R>=r) return trd[bian];pushdown(bian);int res=0;if(L<=mid) res+=query(bian<<1,l,mid,L,R);if(R>mid) res+=query(bian<<1|1,mid+1,r,L,R);return res;
}
int query1(int bian,int l,int r,int L,int R){if(L<=l&&R>=r){if(trm[bian]==0) return trc[bian];return 0;}pushdown(bian);int res=0;if(L<=mid) res+=query1(bian<<1,l,mid,L,R);if(R>mid) res+=query1(bian<<1|1,mid+1,r,L,R);return res;
} 
signed main(){freopen("simulator.in","r",stdin);freopen("simulator.out","w",stdout);n=read();for(int i=1;i<=n;i++) a[i]=read();build(1,1,n);int q=read();while(q--){int op=read();if(op==1){int l=read(),r=read(),x=read();update(1,1,n,l,r,x);}else if(op==2){int l=read(),r=read(),x=read();update1(1,1,n,l,r,x);}else if(op==3){int x=read();update2(1,1,n,x);}else if(op==4){int l=read(),r=read();cout<<query(1,1,n,l,r)<<"\n";}else{int l=read(),r=read();cout<<query1(1,1,n,l,r)<<"\n";}} return 0;
}