引言
进度条部件(lv_bar)
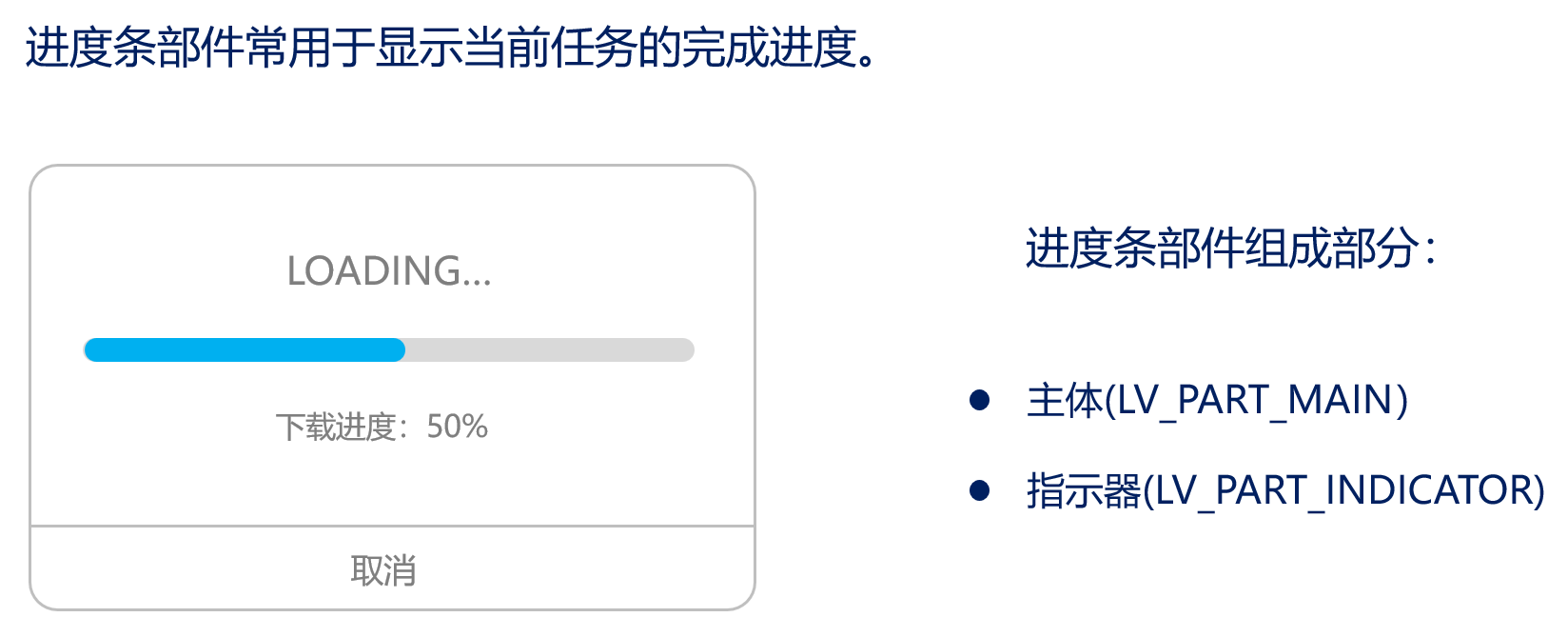
进度条部件相关 api 函数


示例程序
这里建议设置模式为LV_BAR_MODE_RANGE,否则在新版本中,默认模式不可用于设置起始值,容易出问题。
void my_gui(void)
{lv_obj_t *bar = lv_bar_create(lv_scr_act()); /* 创建进度条 */lv_obj_set_align(bar, LV_ALIGN_CENTER); /* 设置对齐 */lv_obj_set_size(bar, 400, 20); /* 设置尺寸 */lv_bar_set_range(bar, -100, 100); /* 设置范围值 */lv_obj_set_style_anim_time(bar, 10000, LV_STATE_DEFAULT); /* 设置动画时间 */// 以上两个设置都必须放在当前值设置之前lv_bar_set_value(bar, 100, LV_ANIM_ON); /* 设置当前值,并开启动画 */lv_bar_set_mode(bar, LV_BAR_MODE_NORMAL); /* 设置模式,默认从最左侧开始绘制 */
// lv_bar_set_mode(bar, LV_BAR_MODE_SYMMETRICAL); /* 设置模式,从零开始绘制到当前值 */
// lv_bar_set_mode(bar, LV_BAR_MODE_RANGE); /* 设置模式,允许设置起始值 */lv_bar_set_start_value(bar, -50, LV_ANIM_OFF); /* 设置起始值,起始值必须小于当前值 */
}
博客导航
博客导航
)



![好题集 (1) - LG P3978 [TJOI2015] 概率论](http://pic.xiahunao.cn/好题集 (1) - LG P3978 [TJOI2015] 概率论)



 Pro v4.8.5.1185 多语便携版)


uvmdvgen)




![B4093 [CSP-X2021 山东] 发送快递](http://pic.xiahunao.cn/B4093 [CSP-X2021 山东] 发送快递)


