完整教程：对于环形链表、环形链表 II、随机链表的复制题目的解析

开篇介绍：

hello 大家，本篇博客依旧为大家带来leetcode中经典单链表算法题的解析，那么我们依旧是废话少说，直接先给上题目链接：141. 环形链表 - 力扣（LeetCode）https://leetcode.cn/problems/linked-list-cycle/description/

142. 环形链表 II - 力扣（LeetCode）https://leetcode.cn/problems/linked-list-cycle-ii/submissions/663494547/138. 随机链表的复制 - 力扣（LeetCode）https://leetcode.cn/problems/copy-list-with-random-pointer/description/

141. 环形链表：

这道题其实不难的，依旧是用我们的快慢指针来解决，但是呢，其中的原理以及扩展，就值得我们去好好探索探索，可有意思了诸位，大家记得复习复习数学

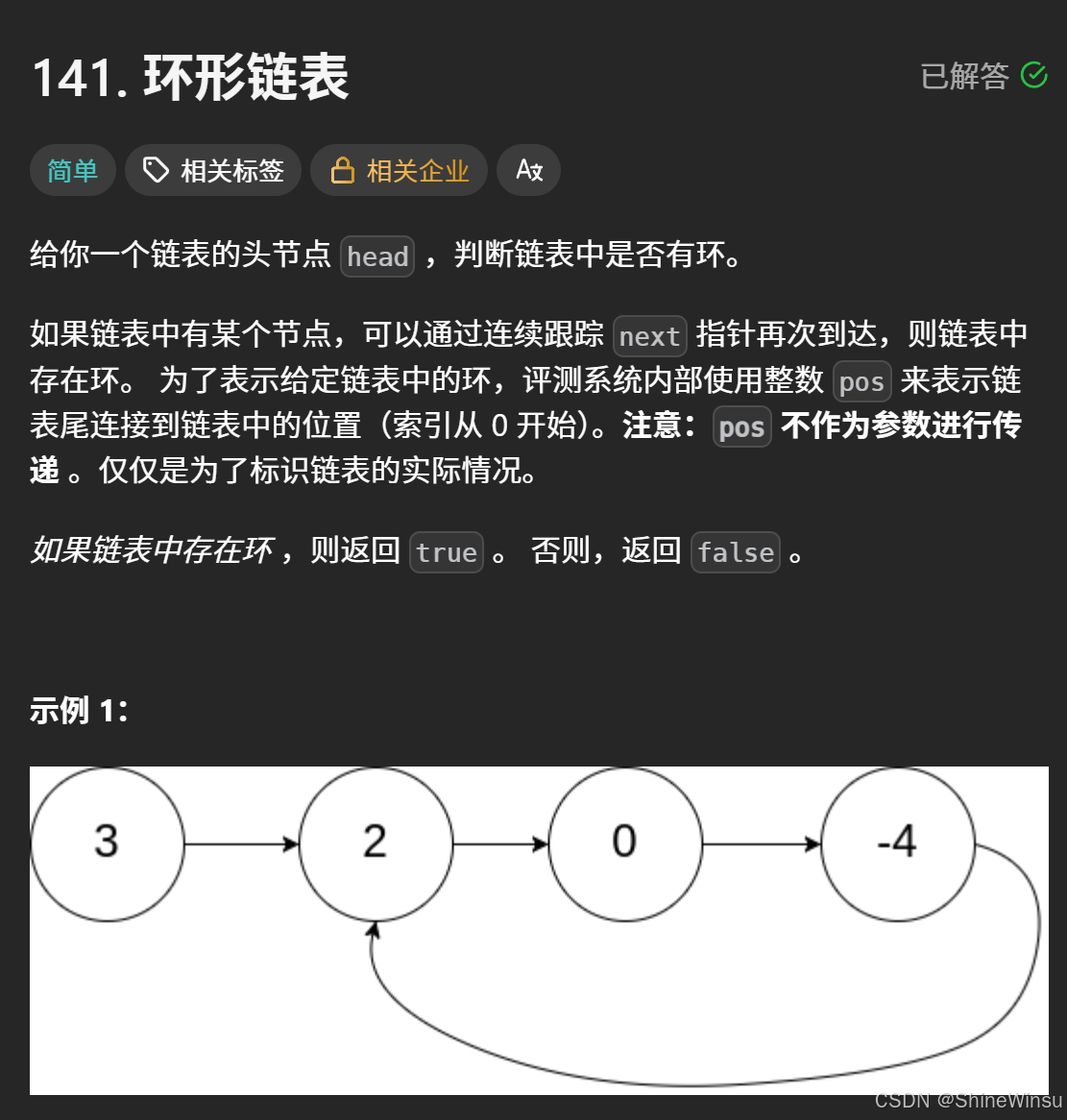
题意分析：

这道题是要判断给定的链表是否存在环。

核心问题

链表的节点通过 next 指针连接，若存在一个节点，能通过连续跟踪 next 指针再次到达它，就说明链表有环。

输入输出

• 输入：链表的头节点 head，以及用于评测系统标识链表实际是否有环及环的位置的 pos（但 pos 不作为参数传入）。
• 输出：若链表有环，返回 true；否则返回 false。

示例理解

• 示例 1 中，链表 3 -> 2 -> 0 -> -4，尾节点 -4 的 next 连接到节点 2，形成环，所以返回 true。
• 示例 2 中，链表 1 -> 2，尾节点 2 的 next 连接到节点 1，有环，返回 true。
• 示例 3 中，链表只有一个节点 1，无环，返回 false。

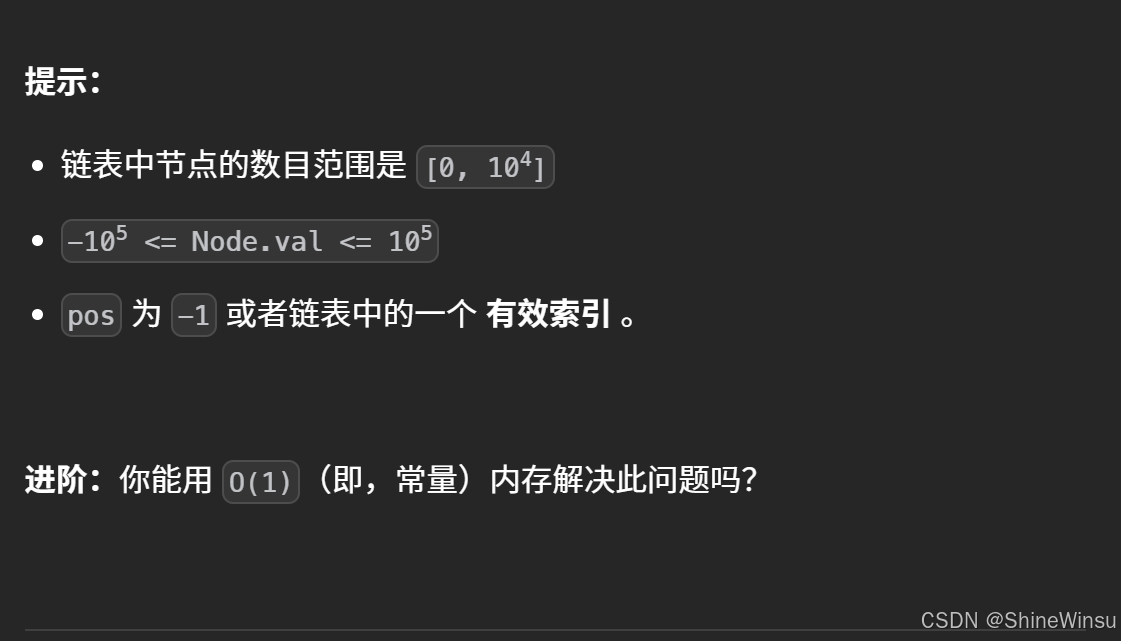
约束条件

• 节点数目范围是 [0, 10^4]。
• 节点值的范围是 [-10^5, 10^5]。
• pos 为 -1（表示无环）或链表中的有效索引（表示有环时尾节点连接的位置）。

进阶要求

要用 O(1)（常量）的内存空间解决问题，这意味着不能使用额外的、与链表长度相关的存储空间，通常可以考虑快慢指针（ Floyd 判圈算法）的方法。

解析:

那么当各位第一眼看到这一道题的时候，其实难免就犯了困难，因为我们只知道它是环形链表，但是究竟有什么方法去判断，而且环形链表长什么样子，有什么性质都不知道，不过没事，题目不是有给我们例图嘛，我们看看：

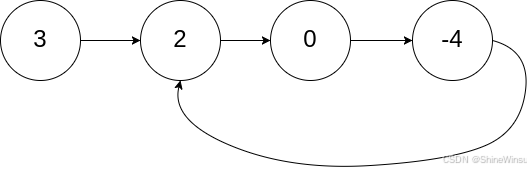
这里提醒一下各位，不要想当然的就认为环形链表是链表的最后一个节点的next指针指向第一个节点，这是不对的，就比如上图，它也是个环形链表，但是它并不是最后一个节点的next指针指向第一个节点。

所以，我们就要仔细思考这么一道题了，那么光看例图感觉很怪，我们不妨直接画图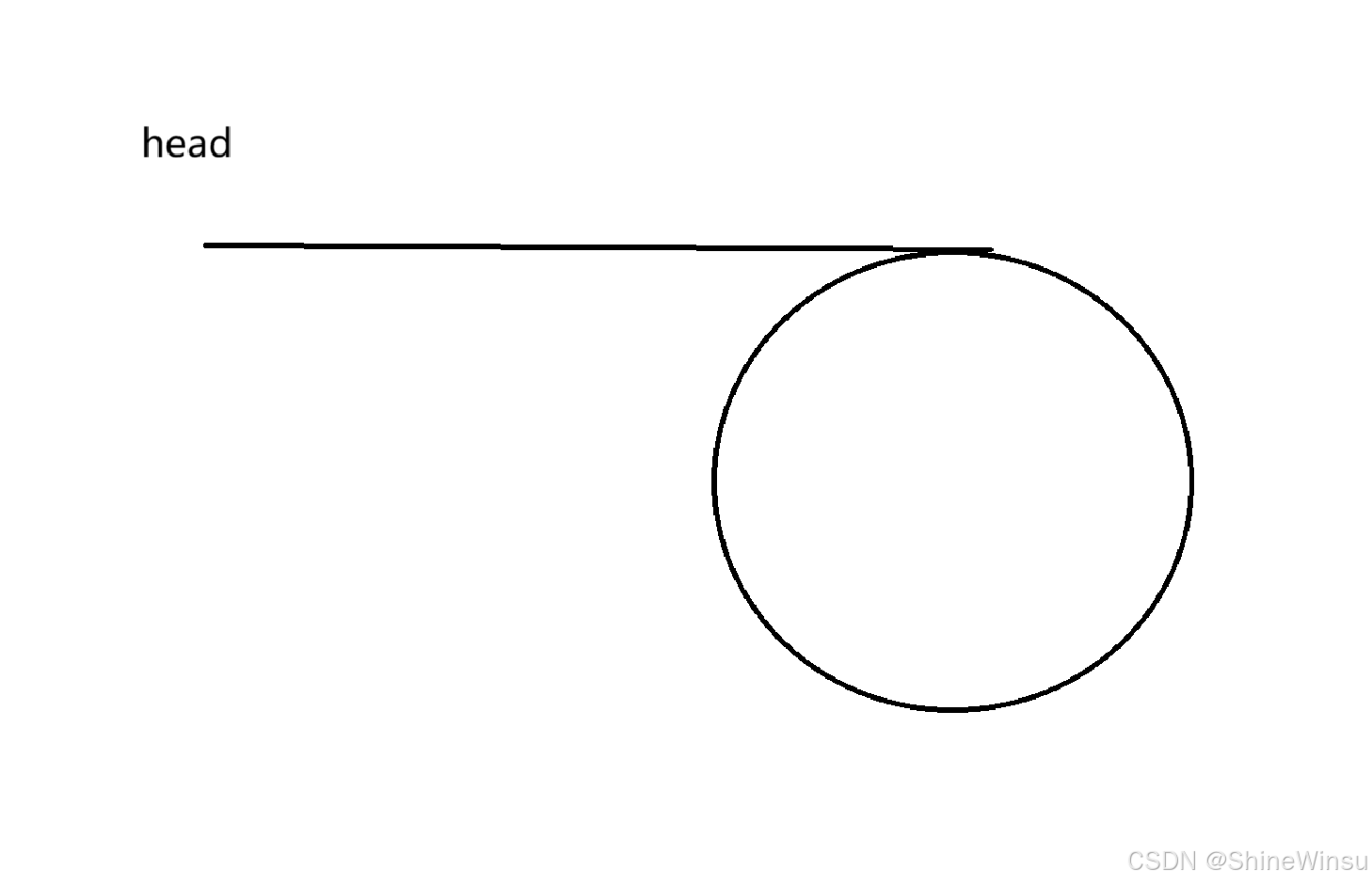：如此即为我们环形链表的粗略图，我们后续的分析都将沿着这幅图进行解析。

那么对于这一道题的解法，我就直接给大家，那就是快慢指针法，是的，又是它，我们依旧设置fast、slow两个指针，然后依旧是fast走两步，slow走一步，那么fast肯定会先进环，而当fast在环里面晃荡的时候，slow可能才抵达环，那么这个时候fast就会开始追击slow，那么大家觉得fast指针追得上slow吗？

答案是，追得上，请你相信fast，也请你相信你自己，追得到的。

具体原理呢，是这么个回事，我们知道，fast肯定会比slow先进环，而当slow进环之后，我们知道，由于fast速度比slow速度快，所以就会形成快追慢的情况，而且由于这是个环，所以就相当于两个人在四百米环形跑道上赛跑，快的一定是能追上慢的人的，至于用数学来解释就是，我们假设slow进环之后，fast和slow相距N，即如下图：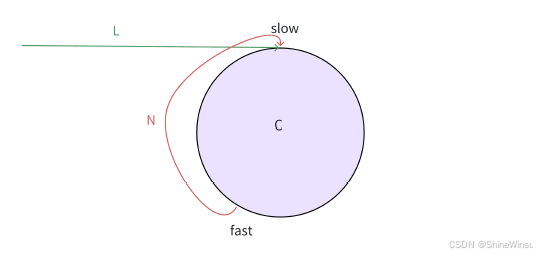

那么我们又知道，fast走两步，slow走一步，那么fast和slow的距离就会减一步（相对运动），那么我们又知道两个指针的距离是N，那么随着运动，就是N-1,N-2,N-3……3 2 1 0，当二者之间的距离为0时，那就是代表二者相遇了，让我们恭喜fast成功追到了slow。

要判断该链表是否为环形链表，我们就可以判断在fast和slow两个指针移动过程中，有没有出现两个指针指向的节点地址一样的情况，有的话就代表是环形链表，那么如果出了移动循环之后，还是没有出现那种情况，就代表不是环形链表。

这便是使用快慢指针解决这道题的原理，我们下面看代码：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     struct ListNode *next;* };*/
typedef struct ListNode sl;
bool hasCycle(struct ListNode *head) {sl* fast=head;sl* slow=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;if(fast==slow){return true;}}return false;
}

那么不知道大家会不会好奇，因为如果是循环链表的话，那我们的while(fast&&fast->next)不是会死循环吗，永远到不了下面的return false吗，那么各位，我觉得有这个想法，也一定是个人才，比如我，我现在在写这篇博客的时候，就突然冒出了这个想法，也是挺牛波一的说实话，哈哈哈。

其实这个问题毫无必要，因为如果是环形链表的话，那么就一定会到

if(fast==slow)
{return true;
}

这一步，而要不是环形链表的话，那么fast就一定最终到NULL，那么这个时候不是也就能到return false了，哈哈哈，我也是挺无语的，会突然有这么个想法。

那么对于这道题，其实我的醉翁之意不在酒，并不是想简单这么讲，我还想讲讲，如果fast指针走3步、4步、5步……呢，那这个时候还一定会追到slow指针吗（slow依旧是移动1步哦）。

我们不妨拿fast走3步作为例子来分析分析，我们依旧假设slow进环后，和fast的距离是N

那么此时随着移动，距离就会这么变化：N-2,N-4,N-6……，（大家这里可一定一定要注意，每移动一次，fast和slow的距离都会减2步，我们上面的累积的结果，准确应该是：N-2,N-2,N-2-2……，大家可千万不要以为是第一次少2步，第二次少4步什么什么的）因为fast比slow多走两步嘛，那么问题就来了，如果N是偶数的话，那可能还行，能追上，这个应该不用我过多解释，大家能理解。

那要是N为奇数呢，啊哦，毋庸置疑，肯定最后结果不为0，比如N=3,N-2=1,1-2=-1，啊哦，结果为负一了，说明fast错过了slow，而且fast还超过了slow一步，就像下图：

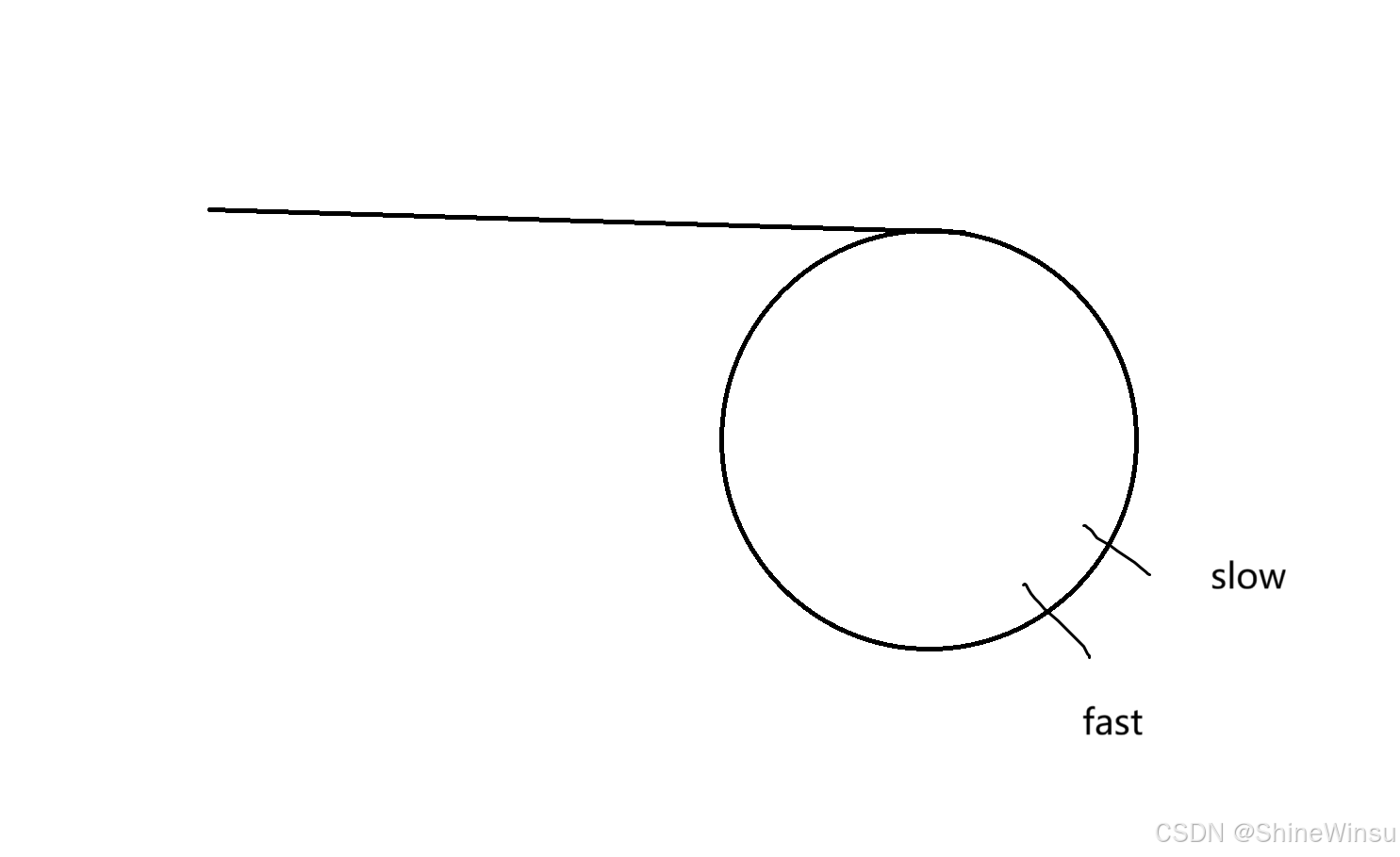
那么这个时候fast和slow之间的距离可就不再是N了，那么是多少呢？是C-1（我们假设环的长度是C），因为fast领先slow一步，那么它们之间的距离可不就是C-1，大家可以再看下图：

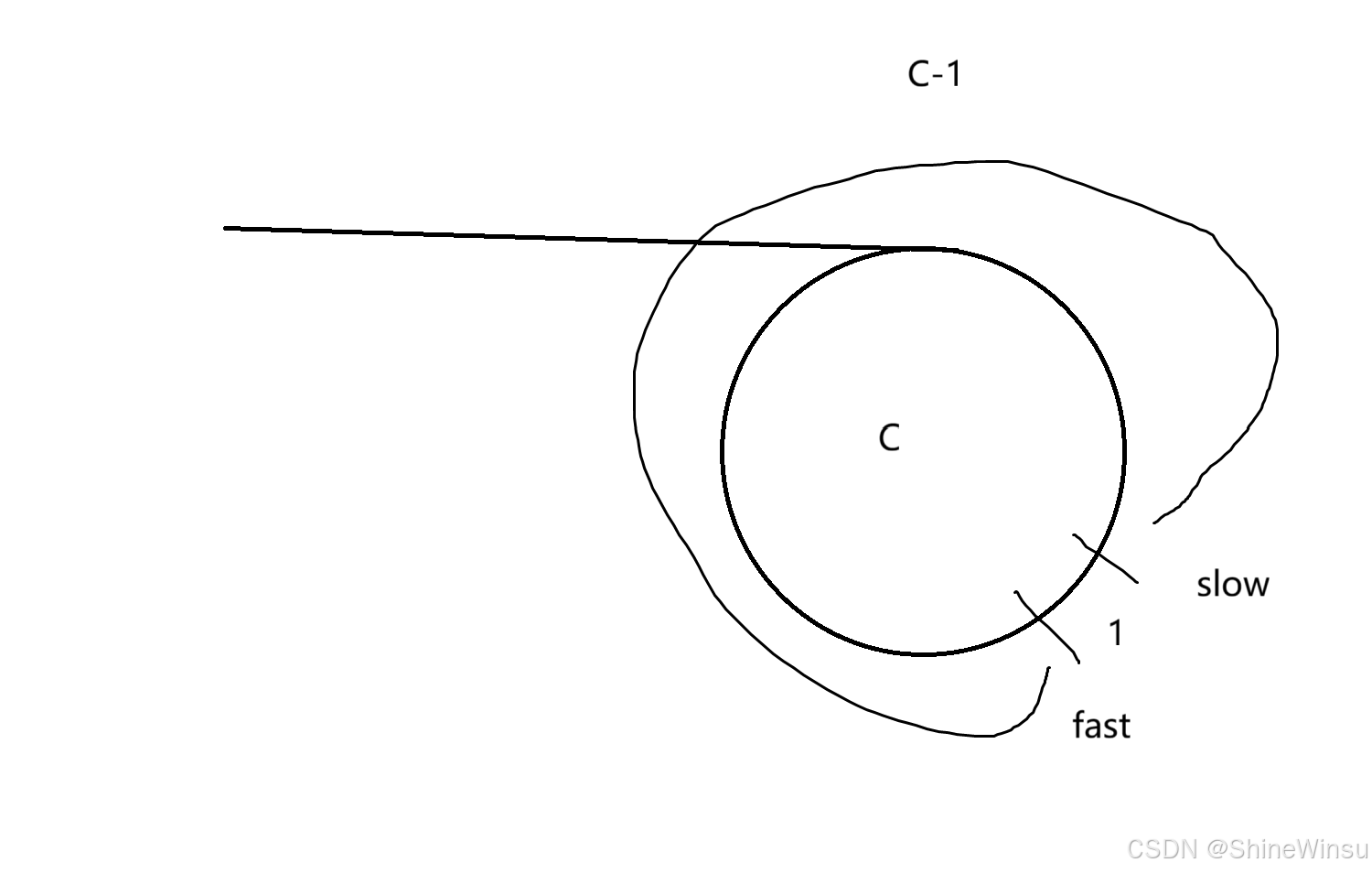大家要注意，因为是fast追得slow，所以是看从fast出发距离slow有多远，而不是看从slow出发距离fast有多远，这个小细节希望大家注意。

那么此时fast和slow的距离就是C-1，而我们依旧是fast领先slow两步，那么随着移动，两个指针的距离就这么变化：C-1-2,C-1-2-2,C-1-2-2-2……（通过这个我们就能看出，C-1不能为奇数），即C-3,C-5,C-7……，那么此时，问题可不就又来了，当C是奇数时，那还好搞，可以为0，可要是C为偶数呢？欧呦，那就又不能追到了。

所以经过上面，我们就知道，当N（fast没有绕圈超了slow时二者之间的距离）为奇数，C（fast有绕圈超了slow时二者之间的距离（C-1））为偶数时，fast就追不到slow。

那么，真的会这样吗？

有没有可能不会出现N（fast没有绕圈超了slow时二者之间的距离）为奇数，C（fast有绕圈超了slow时二者之间的距离（C-1））为偶数这样子的情况呢？

诶，其实还真不会，那么怎么个不会法呢？那就需要大家的数学思维来帮帮忙了。

首先，我们要知道slow走到总路程，我们就假设slow进环之后，这里注意，我们的slow因为是走一步一步的，那么它就一定会走到环的起点，所以我们要拿环的起点进行分析，也就是说，我们要拿slow指针运动到环的起点的这一刻进行分析，因为在这之后，我们的fast指针才算是正式开始追击slow指针了，那么这个时候fast和slow指针之间的距离，才是真正的刚开始的距离，即N，它距离头结点的距离为L，那么slow运动的总路程就是L，而fast因为早就已经进环，并且还可能转了几圈（当然也有可能是几分之几圈），我们就假设是转了x圈吧，那么fast运动的路程是多少呢？先看下图：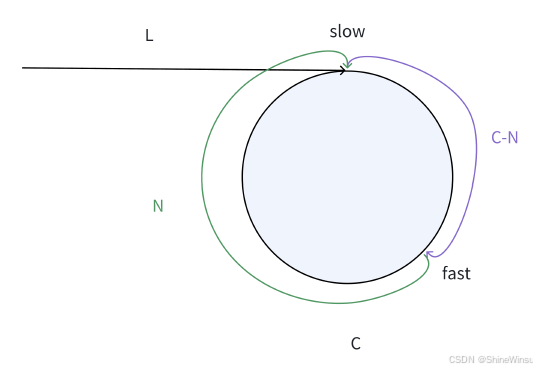

那么这个时候，我们就可以开始分析fast指针所运动的路程（这里再次强调，这里的路程指的是当slow指针运动到环的起点的时候，fast指针所运动的路程），首先，fast路程肯定要算上从头结点到环的起点的距离，即L，之后，还要算上fast指针所运动的x圈，即x*C，但是我们知道，fast所运动的x圈，是指fast从环的起点开始绕圈再到环的起点，而根据上图来看，fast还是要运动C-N的，因为经过x圈，fast才到环的起点，它再移动的距离就是C-N，所以，当slow指针运动到了环的起点时，fast指针运动的距离是L+X*C+C-N，而slow指针运动的距离是L。

接下来，关键就来了，我们知道，因为fast每次运动的步数是slow的三倍，所以说，fast运动的路程就是slow运动路程的三倍，即  L+X*C+C-N==3*L ，那么我们对这个式子进行化简，就变成了2L=X*C+C-N=（x+1）*C-N。

这个式子，就是我们分析的关键。

我们知道，偶数*任何数，结果都会为偶数，那么也就是说2L一定是偶数，又由于等式关系，（x+1）*C-N也一定是偶数，那么我们就按照上面说的N（fast没有绕圈超了slow时二者之间的距离）为奇数，C（fast有绕圈超了slow时二者之间的距离（C-1））为偶数来看，C如果是偶数的话，那么（x+1）*C也一定是偶数，而N如果是奇数的话，那么偶数减奇数，结果不可能为偶数，所以，我们上面所说的N（fast没有绕圈超了slow时二者之间的距离）为奇数，C（fast有绕圈超了slow时二者之间的距离（C-1））为偶数这种情况绝对不存在，所以即使你fast走3步、4步等等，都会遇到slow指针。

当然，我们没必要闲的去让fast不走2步，这是吃力不讨好的事，所以，我们一般都让fast走两步，上面的分析只是为了大家提高提高思维能力。

到了这里，这题的解析就大功告成了诸位。

142. 环形链表 II：

这道题是上一题的难度加大版，但是其实也不难，我们先看题目：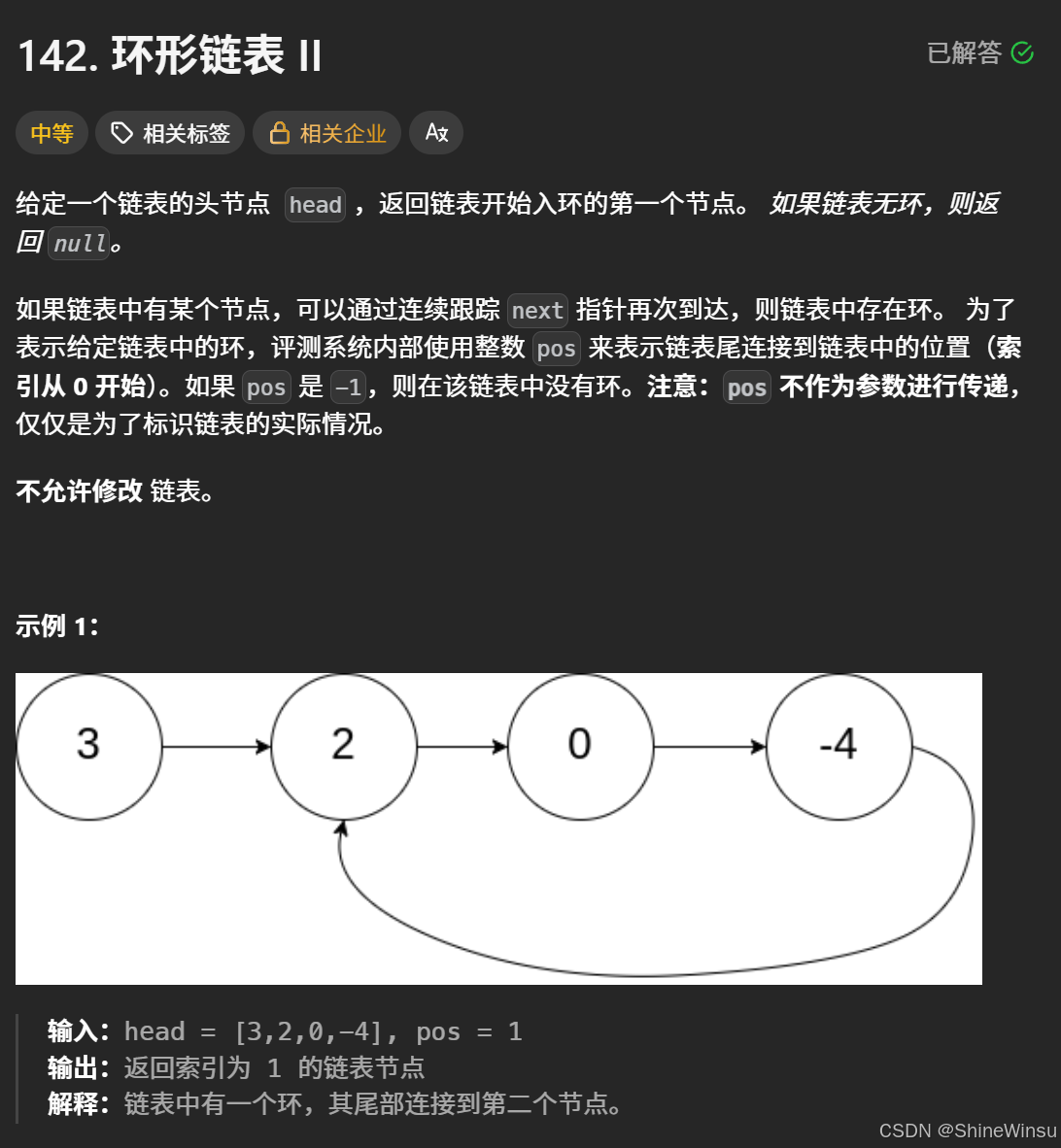

题意分析：

这道题要求我们找到链表中环形的入口节点（若存在环），否则返回null。

• 核心问题：判断链表是否有环，并确定环的入口节点。
• 关键条件：
  • 若链表中存在某个节点，能通过连续跟踪next指针再次到达，就说明链表有环。
  • 用pos（不参与参数传递，仅标识实际情况）表示链表尾连接到链表中的位置（索引从0开始），pos = -1表示无环。
  • 约束条件：节点数目在[0, 10⁴]，节点值范围[-10⁵, 10⁵]，pos为-1或有效索引。
  • 进阶要求：尝试用O(1)空间复杂度解决。

简单来说，就是要在可能存在环的链表中，精准定位环的起始节点，还得考虑空间效率优化。

解析：

其实这道题的需求就是，我们要先判断链表是不是环形链表，那么这一步我们上一题已经实现了，而下一步就是要求我们返回环形链表的起始点，那么对于这一步，我有两个方法：

方法一：

其实这个方法是很暴力的，因为我们知道，当判定为环形链表时，slow和fast在同一个节点，那么我们就可以抓住这个节点，诶，然后怎么办呢？我们把这个节点（假设为meet）的下一个节点保存一下，然后直接把meet->next给它斩断，没错，就是这么残忍，大家可能会好奇为什么要这样子，诶，我给大家看图就知道了：

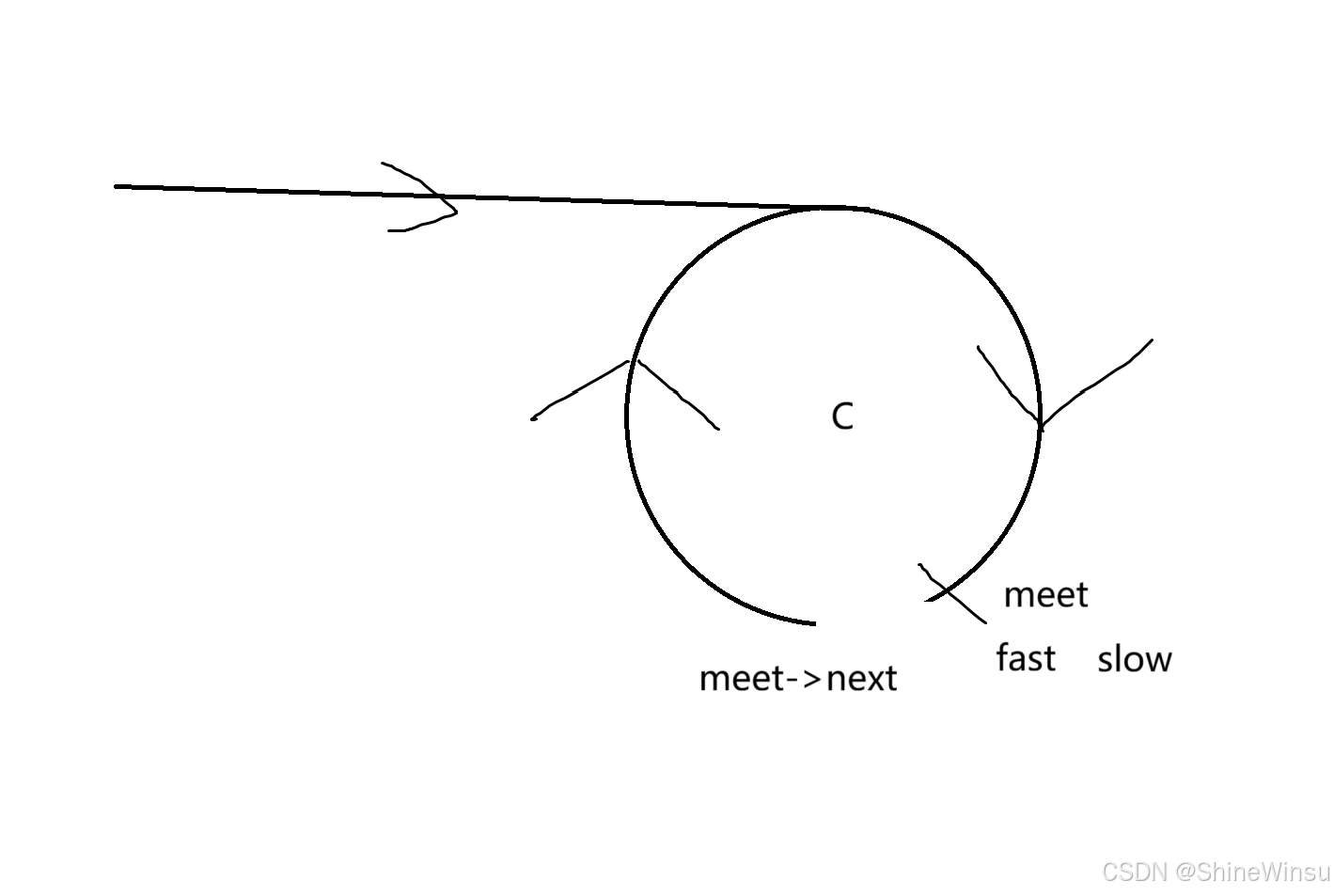
这是斩断之后的链表样子，聪明的你，应该不可能想不到这是什么，很明显，这就是相交链表嘛，是吧，而环形链表的起始节点，可不就是相交链表相交的第一个节点嘛，那如何找到相交链表的第一个相交的节点，我在上一篇有讲到大家直接去看就行，下面我直接给出完整代码：

//直接打断链表，转换为相交链表问题
typedef struct ListNode sl;
sl* findhead(sl* heada,sl* headb)
{int counta=0;int countb=0;sl* cura=heada;sl* curb=headb;while(cura){counta++;cura=cura->next;}while(curb){countb++;curb=curb->next;}sl* longsl=heada;sl* shortsl=headb;int gap=abs(counta-countb);if(countb>counta){longsl=headb;shortsl=heada;}while(gap--){longsl=longsl->next;}while(longsl!=shortsl){longsl=longsl->next;shortsl=shortsl->next;}return longsl;
}
struct ListNode *detectCycle(struct ListNode *head) {
sl* fast=head;
sl* slow=head;
while(fast&&fast->next)
{fast=fast->next->next;slow=slow->next;if(fast==slow){sl* meet=slow;//相遇的节点sl* next=meet->next;meet->next=NULL;return findhead(head,next);}
}
return NULL;
}

为了帮助大家理解，我再给上一版详细注释：

// 将链表节点结构体struct ListNode重命名为sl，简化后续代码书写
// 这里的sl是struct ListNode的别名，提高代码可读性
typedef struct ListNode sl;
/*** 函数功能：寻找两个单链表的相交节点（若存在）* 算法原理：当两个链表相交时，从相交节点开始到链尾的部分完全重合*          通过对齐两链表长度，同步遍历找到第一个相同的节点即为交点* 参数说明：*   heada - 第一个链表的头节点指针*   headb - 第二个链表的头节点指针* 返回值：  两链表的相交节点指针，若不相交则返回NULL*/
sl* findhead(sl* heada, sl* headb)
{// 定义变量记录两个链表的长度int counta = 0;  // 存储heada链表的节点总数int countb = 0;  // 存储headb链表的节点总数// 定义遍历指针，用于统计链表长度（不修改原头节点）sl* cura = heada;  // 遍历heada的临时指针sl* curb = headb;  // 遍历headb的临时指针// 遍历第一个链表，统计节点数量while(cura)  // 当cura不为NULL时继续遍历（未到链尾）{counta++;          // 节点计数+1cura = cura->next; // 指针移动到下一个节点}// 循环结束后，counta即为heada链表的长度// 遍历第二个链表，统计节点数量while(curb)  // 当curb不为NULL时继续遍历{countb++;          // 节点计数+1curb = curb->next; // 指针移动到下一个节点}// 循环结束后，countb即为headb链表的长度// 定义指针分别指向较长链表和较短链表的头节点sl* longsl = heada;   // 初始假设heada为较长链表sl* shortsl = headb;  // 初始假设headb为较短链表// 计算两链表的长度差（绝对值确保为非负数）int gap = abs(counta - countb);// 若实际headb更长，则交换longsl和shortsl的指向if(countb > counta){longsl = headb;   // 修正为headb是较长链表shortsl = heada;  // 修正为heada是较短链表}// 此时longsl一定指向较长链表，shortsl指向较短链表// 将较长链表的指针向前移动gap步，使两指针处于"同一起跑线"// （即剩余未遍历的节点数相同）while(gap--)  // 循环执行gap次（每次gap减1，直到0）{longsl = longsl->next;  // 长链表指针后移一步}// 移动后，longsl和shortsl到各自链尾的距离相等// 同步遍历两个链表，寻找第一个相同的节点（相交节点）while(longsl != shortsl)  // 当两指针不指向同一节点时继续遍历{longsl = longsl->next;  // 长链表指针后移一步shortsl = shortsl->next; // 短链表指针后移一步}// 循环结束条件：// 1. 两指针指向同一节点（找到相交节点）// 2. 两指针都为NULL（两链表不相交）// 返回找到的相交节点（或NULL）return longsl;
}
/*** 函数功能：检测链表中是否存在环，并返回环的入口节点* 算法核心：*   1. 先用快慢指针判断是否有环（若相遇则有环）*   2. 若有环，将环打断转换为"两个单链表相交"问题，求交点即为环入口* 参数说明：*   head - 链表的头节点指针* 返回值：  环的入口节点指针，若不存在环则返回NULL*/
struct ListNode *detectCycle(struct ListNode *head) {// 定义快慢指针，初始都指向头节点sl* fast = head;  // 快指针：每次移动2步sl* slow = head;  // 慢指针：每次移动1步// 遍历链表，判断是否存在环// 循环条件：fast和fast->next都不为NULL（确保快指针能移动2步）while(fast && fast->next){fast = fast->next->next;  // 快指针移动2步slow = slow->next;        // 慢指针移动1步// 若快慢指针相遇，说明链表存在环（快指针绕环追上慢指针）if(fast == slow){// 记录快慢指针相遇的节点（环内的某个节点）sl* meet = slow;// 保存相遇节点的下一个节点（环中meet之后的部分）sl* next = meet->next;// 关键操作：打断环！将meet的next指针置为NULL// 此时原环形链表被拆分为两个单链表：// 1. 从head到meet（无环部分 + 环的前半部分）// 2. 从next到原环的入口（环的后半部分）// 这两个单链表的相交节点就是原环的入口节点meet->next = NULL;// 调用findhead函数寻找两个单链表的相交节点，即为环的入口return findhead(head, next);}}// 若循环结束仍未相遇，说明链表无环，返回NULLreturn NULL;
}

方法二：

这个方法啊，那就又是数学功底了，其实我们今天的题目，基本都是数学功底，ps：I love math

这个方法的思路很简单，那就是我们让slow和fast相遇的节点，我们定位为meet，然后我们再找到链表最开始的起点，定位为head，然后我们就让head和meet同时向后移动，一步一步的移动，最后它们一定可以相遇到环形链表的起始节点，我们看图：

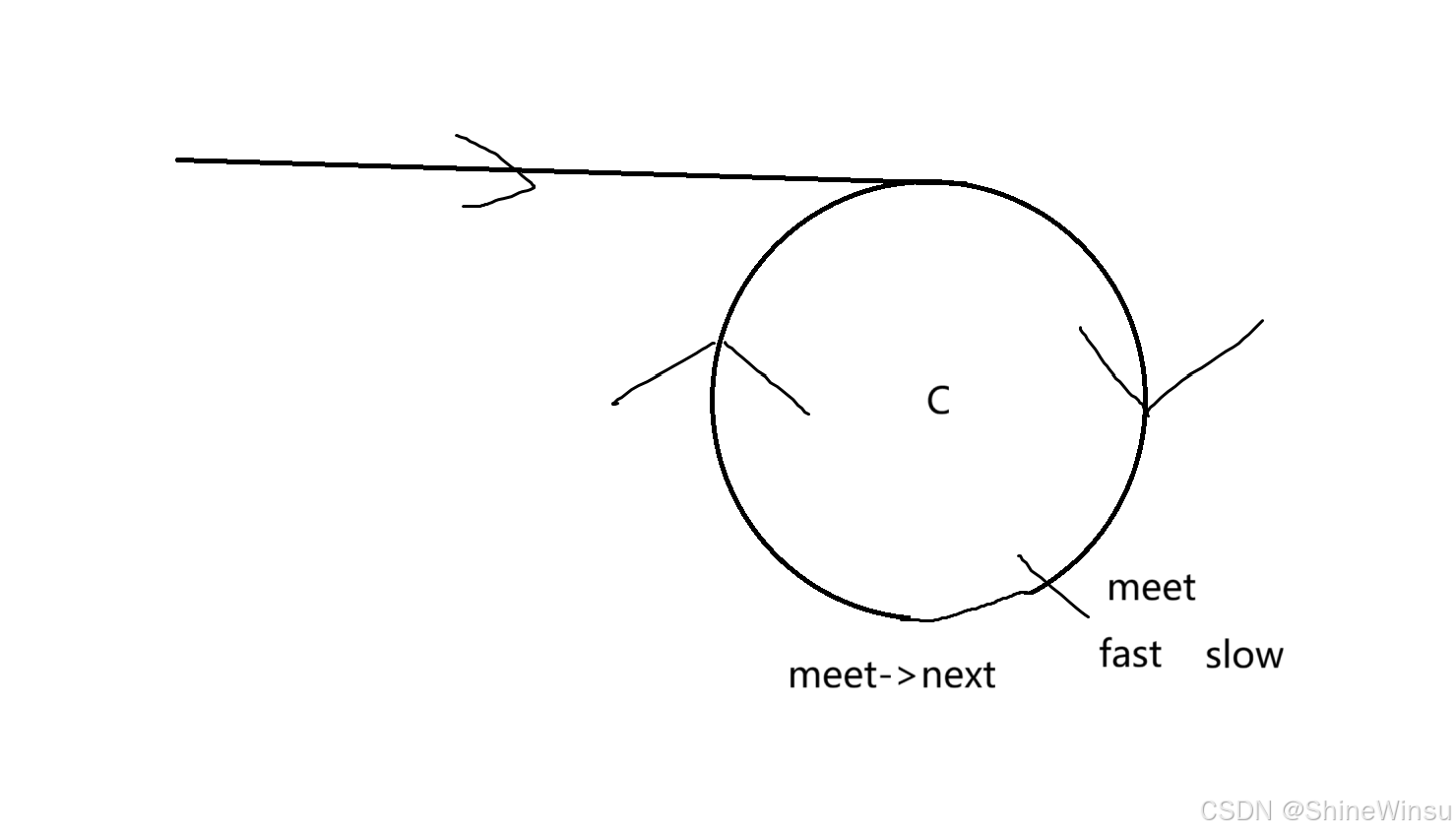
原理我后面会解释，我们先看代码：

//数学思维：
typedef struct ListNode sl;
struct ListNode *detectCycle(struct ListNode *head) {
sl* fast=head;
sl* slow=head;
while(fast&&fast->next)
{fast=fast->next->next;slow=slow->next;if(fast==slow){sl* meet=slow;//相遇的节点sl* cur=head;while(cur!=meet){cur=cur->next;meet=meet->next;}return meet;}
}
return NULL;
}

再给上详细注释：

// 将链表节点结构体struct ListNode重命名为sl，简化代码书写
// 此处的sl作为struct ListNode的别名，使后续代码更简洁
typedef struct ListNode sl;
/*** 函数功能：检测链表中是否存在环，并返回环的入口节点* 算法本质：利用快慢指针的数学特性，通过一次相遇和一次同步遍历找到环入口* 核心优势：时间复杂度O(n)，空间复杂度O(1)，无需额外数据结构* 参数说明：*   head - 链表的头节点指针（可能为空）* 返回值：*   若存在环，返回环的入口节点指针；若不存在环，返回NULL*/
struct ListNode *detectCycle(struct ListNode *head) {// 定义快指针：每次移动2步，用于快速遍历并与慢指针形成速度差sl* fast = head;// 定义慢指针：每次移动1步，用于与快指针配合检测环sl* slow = head;// 遍历链表，判断是否存在环// 循环条件：fast和fast->next都不为NULL（确保快指针能移动2步）// 若fast为NULL或fast->next为NULL，说明链表无环（已到达尾部）while (fast && fast->next) {fast = fast->next->next;  // 快指针移动2步slow = slow->next;        // 慢指针移动1步// 当快慢指针指向同一节点时，说明链表存在环（快指针追上慢指针）if (fast == slow) {// 记录快慢指针相遇的节点（该节点一定在环内）sl* meet = slow;// 定义一个新指针cur，从链表头节点开始移动sl* cur = head;// 核心数学逻辑：头节点到环入口的距离 = 相遇点到环入口的距离（沿环移动）// 详细推导：// 设：// - a = 头节点到环入口的距离（节点数）// - b = 环入口到相遇点的距离（节点数）// - c = 环的总长度（节点数）//// 慢指针走过的距离：a + b（未绕环，因为快指针先进入环并追上）// 快指针走过的距离：a + b + k*c（k≥1，绕环k圈后追上慢指针）//// 由于快指针速度是慢指针的2倍，相同时间内路程也是2倍：// 2*(a + b) = a + b + k*c// 化简得：a + b = k*c → a = k*c - b//// 等式右边的含义：从相遇点继续移动(k*c - b)步 = 从相遇点移动(c - b)步（因k*c是整圈，可忽略）// 即：头节点到入口的距离(a) = 相遇点到入口的距离(c - b)//// 因此，当cur从头部移动、meet从相遇点移动时，两者会在入口节点相遇// 同步移动cur和meet指针，直到它们指向同一节点while (cur != meet) {cur = cur->next;   // cur从头部向入口移动meet = meet->next; // meet从相遇点向入口移动（沿环）}// 当两指针相遇时，所在节点就是环的入口return meet;}}// 若循环结束仍未相遇，说明链表无环，返回NULLreturn NULL;
}

数学原理：

下面我来解释一下这个方法的原理：

我们依旧是需要画图分析，

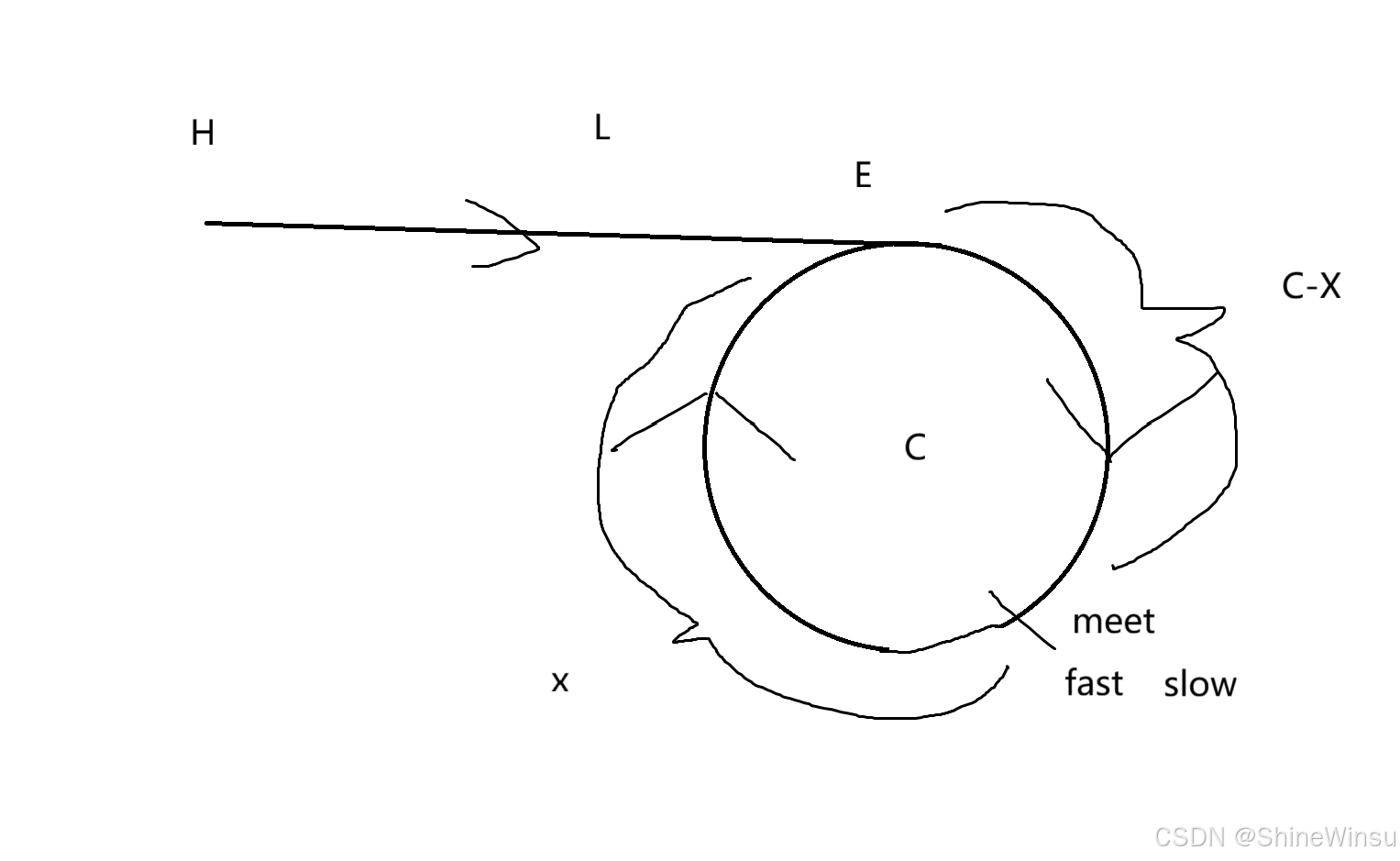
H为链表最开始的起点，E为环形链表的起始阶段，meet即slow和fast相遇时的节点，而x是meet节点离E的距离，E到meet的距离则是C-X。

那么那么那么，我们又要来上数学课了家人们，我们要对上面的思路进行解析，那就肯定要和L与X息息相关，那么怎么样才能把它们两个联系起来呢？其实这就又和我们fast指针和slow指针运动的路程关系有关了。

我们这次是以两个节点相遇时各自所移动的路程为关系。

首先还是slow指针，它的运动路程是多少呢？其实看图很容易看出来，是L+C-X，那么这个时候就有人有问题了，主播主播，万一slow指针搁那转圈了后面才相遇呢？其实这是不会的，因为：

要理解 “慢指针进环后，快指针必在慢指针走一圈内追上”，核心是拆解慢指针进环时的初始距离与快慢指针的速度差导致的距离缩减规律，下面用 “环形跑道追及模型” 分步详细解释：

一、先明确前提：慢指针进环时的状态

在慢指针（速度 1 步 / 次）刚进入环的那一刻，我们可以确定两个关键状态：

1. 快指针的位置：
   因为快指针速度是慢指针的 2 倍，慢指针从头部走到环入口用了a步（a是头到环入口的距离），所以快指针此时已经走了2a步。
   由于2a = a + a，这意味着快指针在慢指针进环时，已经从头部出发、经过环入口后，在环内额外走了a步（可能绕环 0 圈或多圈，但最终停在环内某个位置）。

2. 快慢指针的初始距离（环内）：
   设环的长度为c（环内总节点数）。此时快慢指针都在环内，它们之间的 “环内距离” 可以理解为：快指针要追上慢指针，需要多走的步数（沿环的顺时针 / 逆时针方向，取较短的那段）。
   关键结论：这个初始距离最大不会超过c-1（因为环的总长度是c，两个点在环上的最大距离就是 “差一步绕完一圈”，比如环有 5 个节点，两点最远隔 4 步）。

二、核心逻辑：速度差导致距离 “步步缩减 1”

快慢指针的速度分别是：

• 慢指针：1 步 / 次（每轮循环移动 1 个节点）
• 快指针：2 步 / 次（每轮循环移动 2 个节点）

每一轮循环（即快慢指针各移动一次），两者的距离变化是：
快指针比慢指针多走 1 步 → 相当于 “快慢指针之间的环内距离，每轮缩减 1 步”。

举个具体例子：
假设慢指针进环时，快慢指针的初始距离是d（d ≤ c-1）：

• 第 1 轮：距离从d → d - (2-1) = d-1
• 第 2 轮：距离从d-1 → d-2
• ...
• 第d轮：距离从1 → 0（追上）

三、结论：慢指针走不满一圈就会被追上

从上面的推导可知：

1. 慢指针进环后，需要走d步才能被追上（d是初始环内距离，d ≤ c-1）。
2. 慢指针走d步，意味着它在环内移动的距离是d，而d ≤ c-1（小于环的总长度c）。

这就相当于：慢指针在环内刚走了 “不到一圈”，快指针就已经通过 “每轮多走 1 步” 的速度差，把初始距离缩减到 0，实现了追上。

用生活场景类比：环形跑道追及

假设两人在 400 米环形跑道上跑步：

• 慢人速度 1 米 / 秒，快人速度 2 米 / 秒。
• 慢人刚进入跑道时，快人已经在跑道内，两人最多相距 399 米（不到一圈）。
• 每秒钟，快人比慢人多跑 1 米 → 399 秒后就能追上。
• 此时慢人只跑了 399 米（不到 400 米，即不满一圈），快人跑了 798 米（1 圈 + 398 米）。

这个场景和链表追及完全一致：快指针的 “2 倍速度” 转化为 “每轮多走 1 步” 的优势，而初始距离不超过环长，最终必然在慢指针走满一圈前追上。

为什么这个结论重要？

它排除了 “慢指针绕环多圈后才被追上” 的可能性，证明了快慢指针的相遇点一定在慢指针的 “第一圈环内”，这也是后续 “数学推导找环入口” 的重要前提（确保慢指针的路程是a+b，而非a+b+k*c，简化了等式）。

所以，我们知道，slow走到相遇时运动的路程是L+C-X

那么fast运动的路程呢？它就肯定要走几圈了，我们假设走m圈，那么其实fast运动的路程就是L+m*C+C-X，那么这里大家依然要注意，fast绕圈运动的起始点我们是按照E开始的，绕一圈是回到E，随后再走C-X到meet。

那么这个时候，我们就可以得出两个路程的关系式了，因为fast的速度是slow的两倍，所以，2*（L+C-X）==L+m*C+C-X，我们化简一下就是L+C-X=m*C，再化简就是L=(m-1)*C+X。

那么呢吧，我们知道，(m-1)*C其实就是绕圈圈，可有可无，所以如果我们忽略(m-1)*C的话，能忽略的原因如下：

要理解 “为什么能忽略 (m-1)*C（C 是环长，m 是快指针绕环圈数）”，核心是抓住 “环形结构中‘整圈移动’不改变相对位置” 这一本质特性 —— 绕环整数圈后，指针相当于回到了 “等效起点”，对最终要找的 “环入口位置” 没有影响。下面从数学意义、物理类比、算法目标三个维度拆解：

一、先回顾推导背景：(m-1)*C 是怎么来的？

在快慢指针相遇的数学推导中，我们曾得到关键等式：
a = m*C - b（a= 头到环入口距离，b= 环入口到相遇点距离，m≥1）

将等式变形后：
a = (m-1)*C + (C - b)

这里的 (m-1)*C 表示 “从相遇点出发，绕环 m-1 整圈”；(C - b) 表示 “从相遇点出发，不绕整圈、直接走到环入口的距离”。

二、核心原因：环形结构中 “整圈移动” 是 “无效位移”

环形的本质是 “没有起点和终点，绕整圈后位置不变”—— 就像在 400 米跑道上跑 1 圈、2 圈、m-1圈，最终还是回到起点，没有产生 “额外的位置变化”。

具体到指针移动：
假设环长 C=5，相遇点在环内第 3 个节点（从入口开始数），那么 C - b = 5 - 3 = 2（从相遇点走 2 步到入口）。
如果 m=3（快指针绕环 3 圈后追上），则 (m-1)*C = 2*5=10：

• 从相遇点先绕 2 整圈（10 步），指针回到相遇点；
• 再走 C - b=2 步，到达入口。

可见：绕 (m-1) 整圈的操作，只是让指针在环内 “空跑”，最终还是要走 C - b 步才能到入口。
(m-1)*C 不会改变 “相遇点到入口的有效距离”，它的存在与否，不影响 “从相遇点到入口需要走 C - b 步” 这个核心结论。

三、结合算法目标：我们只关心 “最终相遇位置”，不关心 “绕了多少圈”

算法的目标是让 “从头部出发的指针 cur” 和 “从相遇点出发的指针 meet” 相遇在环入口。根据推导：

• cur 要走 a 步到入口；
• meet 要走 a = (m-1)*C + (C - b) 步到入口。

但 meet 移动时，我们不需要刻意让它先绕 m-1 圈 —— 因为指针移动是 “连续的”：
当 meet 从相遇点开始移动时，每绕 1 圈（C步）就会回到原位，再继续移动 C - b 步，最终还是会到入口。
而 cur 从头部移动 a 步到入口的过程中，meet 恰好会在 “绕 m-1 圈 + 走 C - b 步” 后，和 cur 同时到达入口。

简单说：(m-1)*C 是 meet 移动过程中的 “冗余路径”，但它不影响 “两指针最终在入口相遇” 的结果—— 就像两个人约定在终点见面，一个人绕了几圈再去终点，另一个人直接去终点，只要总路程对应，依然会同时到达。

四、用具体例子验证：忽略 (m-1)*C 不影响结果

假设：

• 环长 C=5，a=3（头到入口 3 步），b=2（入口到相遇点 2 步）；
• 快指针绕环 m=2 圈后追上，此时 a = 2*5 - 2 = 8？不对，重新代入正确推导：
  慢指针路程 a+b=3+2=5，快指针路程 2*5=10，快指针绕环 (10 - 3)/5 = 1.4 圈 → m=1（绕 1 整圈），则 a = 1*5 - 2 = 3（和实际 a=3 一致）。

若 m=3（快指针绕 3 圈），则 a = 3*5 - 2 = 13？但实际 a=3，这时候 (m-1)*C=2*5=10，a = 10 + (5-2) = 13—— 但 cur 从头部走 13 步：前 3 步到入口，之后绕 2 圈（10 步），还是回到入口；meet 从相遇点走 13 步：绕 2 圈（10 步）+ 走 3 步（C - b=3），也回到入口。

可见：无论 m 是多少，(m-1)*C 只是让指针多绕了几圈，但最终还是会和 cur 在入口相遇 —— 所以在推导时，我们可以直接忽略 (m-1)*C，只关注核心的 C - b，因为它才是决定 “相遇位置” 的关键。

总结：为什么能忽略 (m-1)*C？

因为 (m-1)*C 代表 “绕环整数圈”，在环形结构中，这种移动不会改变指针的 “目标方向”（到入口的距离），也不会影响 “两指针最终在入口相遇” 的结果 —— 它是算法中的 “冗余信息”，忽略后能更清晰地看到核心规律：头到入口的距离 = 相遇点到入口的距离（不绕整圈）。

，那式子就是L=X，那么这不正好就满足meet到环形链表的起始节点的距离X等于链表最开始的起始点到环形链表的起始节点的距离L，由此，我们就解决了。

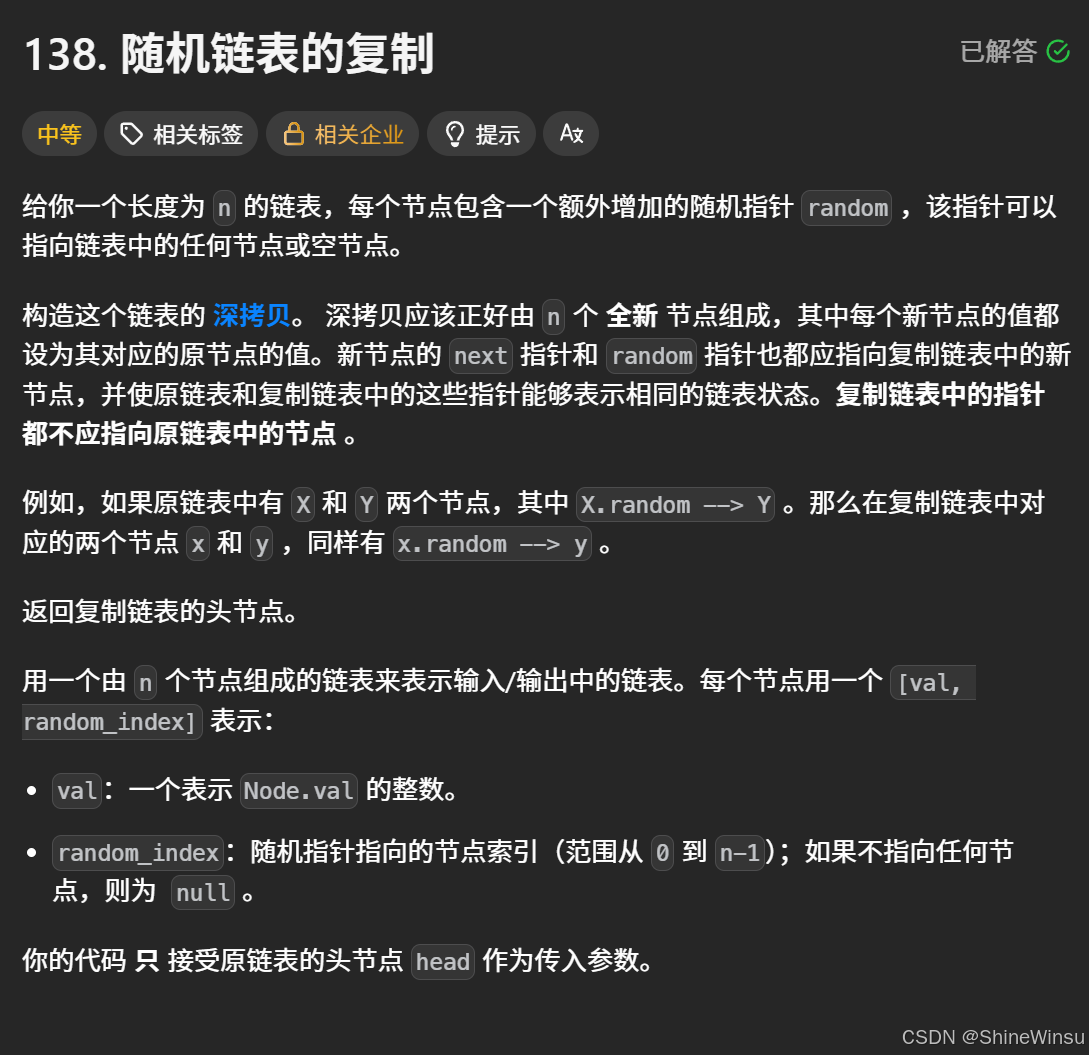
138. 随机链表的复制：

wos，这道题可就了不得喽，很有难度的一道题，我们先看题目：

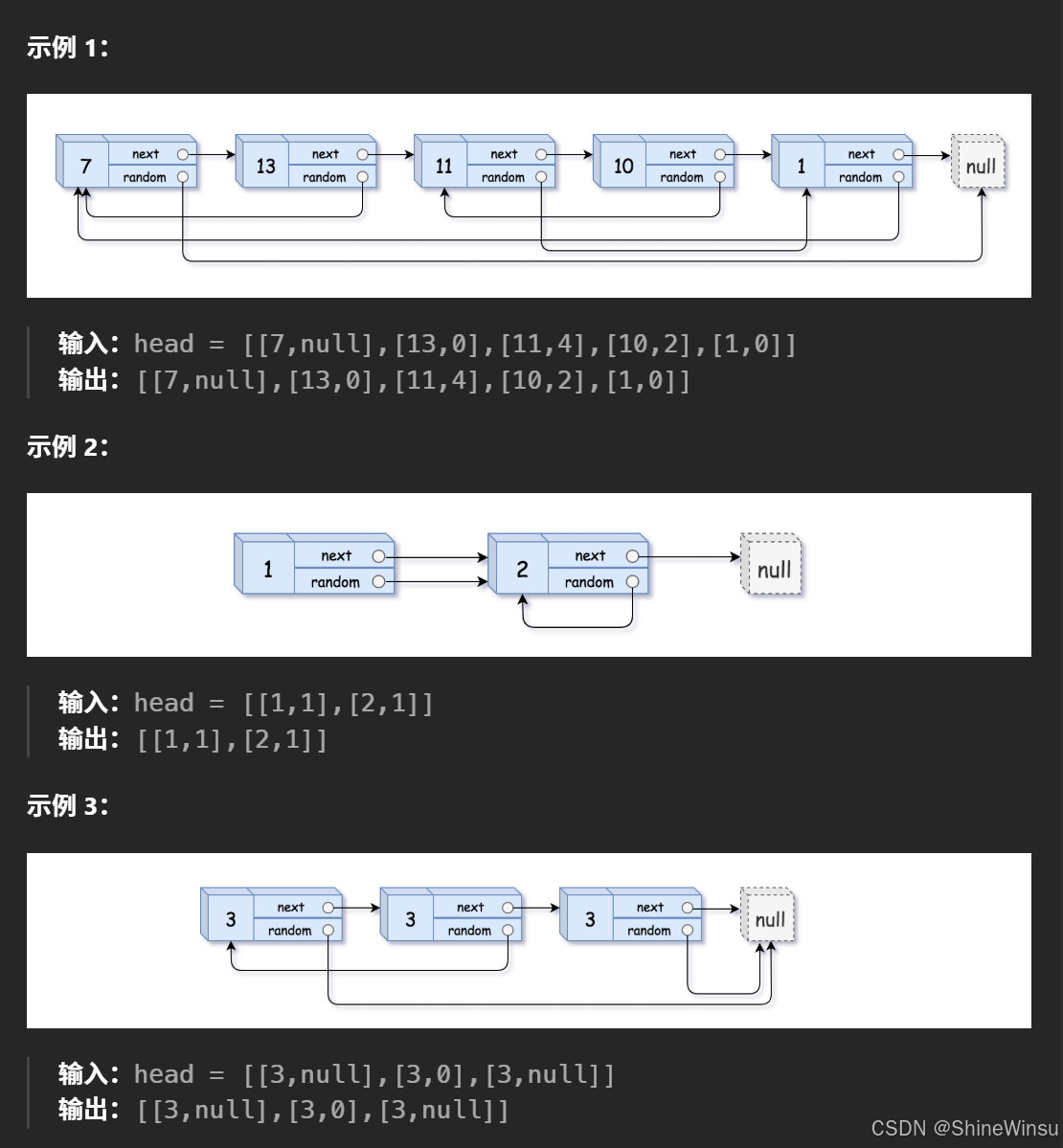
题意分析：

这道题要求我们对带有随机指针（random）的链表进行深拷贝。

• 核心任务：创建一个与原链表完全独立的新链表，新链表的每个节点不仅值与原节点相同，next 指针和 random 指针的指向关系也要与原链表一致，且新链表的指针不能指向原链表的节点。
• 关键要点：
  • 原链表每个节点有 val（值）、next（指向下一节点）、random（指向链表中任意节点或空）三个部分。
  • 深拷贝需保证新链表的 next 和 random 指针都指向新链表自身的节点，与原链表无任何指针关联。
  • 输入用 [val, random_index] 形式表示节点，random_index 是随机指针指向节点的索引（从 0 开始），为 null 则表示不指向任何节点。

简单来说，就是要复刻原链表的结构和指针指向关系，生成一个全新的、独立的链表副本。

解析：

我们依旧是看图说话：

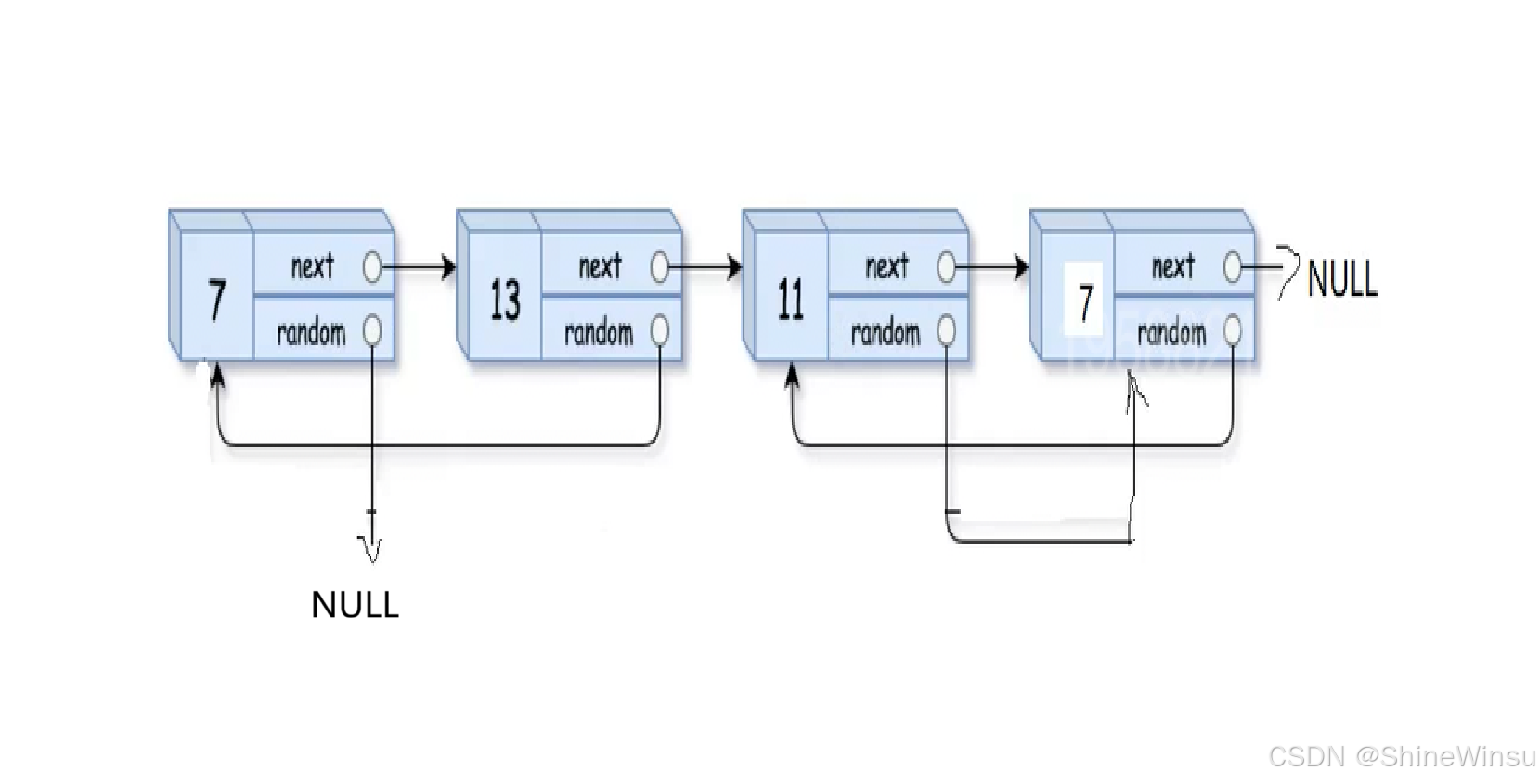
这里我们改编一下题目所给例题，在这里我也不啰嗦太多，我直接给大家目前阶段的最优方法。且看下文：

首先，我们要不断创建节点，即拷贝和原链表节点一样的的节点，然后我们要把这个节点插在它所拷贝的节点后面，同时这个节点的next指针要指向被拷贝节点的下一个节点，具体就是这么个图：

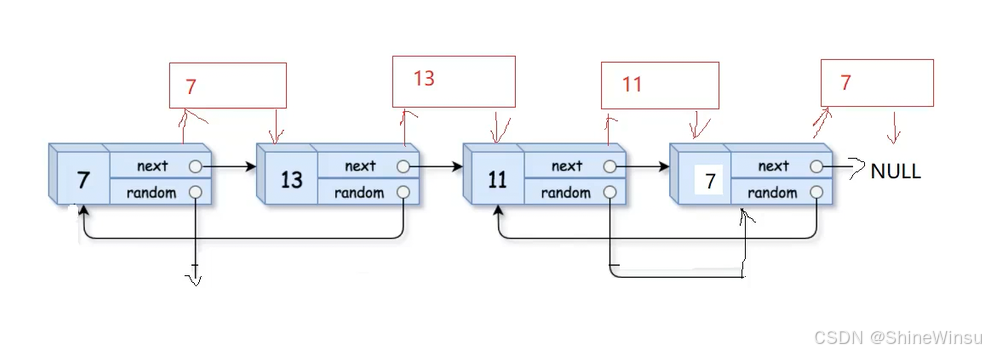
大家对这个应该是不陌生，老生常谈的东西了，只不过在这里我还是想提醒一下各位，在插入新节点时，要记得保存被拷贝节点的next指针哦，不难可就找不到了，后续的不断插入也就无法实现。

那么在我们将原链表的所有节点都拷贝并插入之后，我们就可以开始处理random指针了，它才是我们本题的重难点。

那么要怎么处理呢，其实非常巧妙，大家注意，我们对拷贝节点的random的怎么处理，是看被拷贝节点的random指针的，那么我们究竟要怎么处理呢？

我们不妨拿一个例子来进行分析，有时候偶然性是会成为必然性的。

我们就看我们拷贝的第一个节点7，它的random我们要怎么处理呢，可以知道，要进行拷贝，那么我们的上面的第一个7，它的random指针就要和下面第一个的7这个节点的random指针指向一样，

那么这个时候我们看，下面第一个的7这个节点的random指针指向NULL，那么我们的上面的第一个7的random指针指向也得为NULL，这是第一种情况，当被拷贝节点的random指针指向NULL时，那么还有第二种情况，这个才是重中之重。

我们拿上面的第一个13来分析，它的random指针应该要和下面的第一个13的random指针指向一样，可以看到下面的第一个13的random指针是指向下面的第一个7这个节点，那么我们上面的第一个13的random指针也应该是指向上面的第一个7那个节点，这里要和大家强调一下，可不要误以为上面的第一个13的random指针应该是指向下面的第一个7那个节点，那可就乱了，虽然上下两个链表还连着，但是我们要把它们当做两个来看待，毕竟我们后面是会将上面那个链表单独垃出来的。

言归正传，那么我们要怎么让上面的第一个13的random指针也应该是指向上面的第一个7那个节点呢？这个时候我们可以看看图

能够有所关联的，就是下面的第一个13的random指针指向的下面第一个7的next指针，也就是13->random->next，只有这样，我们才能将这两个链接起来。

所以当被拷贝节点的random指针指向不为空时，我们就得让拷贝节点的random指针=被拷贝节点的random的next。

那么知道了上面所说的之后，我们剩下的就是指针的移动了。

我们在遍历下面的链表时，我们要让上面的链表的random指针正常指向（即如上面所说的），我们就得设置两个指针，假设为cur和copy，cur指向我们下面那个链表的节点，而copy则指向我们上面那个链表的节点，而且要相对应，比如当cur为下面的第一个7时，copy就得为上面的第一个7，这样子才能合理的解决random指针，那么我们操控cur和copy两个指针的移动就至关重要了。

首先，起始的时候，我们肯定要让cur指向下面链表的第一个节点，而copy就要指向上面链表的第一个节点，其实也就是上下总链表的第二个节点，而其正好是下面第一个节点next,那么我们也就是要copy=cur->next。

所以在后续的移动中，我们都要那么移动，而且一定要保持cur始终指向下面链表的节点，而copy要始终指向上面链表的节点，也就是copy要=cur->next。

但是我们要怎么保持cur始终指向下面链表的节点呢？其实也不难，我们可以看图，copy的next指针不就指向下面的链表节点吗，所以我们移动cur就可以cur=copy->next，如此就可以完美解决。

但是有个小问题，那就是在上下总链表中，我们的copy移动速度是会比cur更快一步的，比如当cur移动到如图中最后的NULL时，那么这个时候循环还不会终止，也就是copy依旧是copy=cur->next，这么一来，就会造成空指针范访问，所以为了避免这个情况，我们要进行判断，一旦cur是NULL，我们就得终止循环，避免copy空指针访问，还有就是我们的cur的移动要在copy移动的前面，这个顺序不能乱，具体是为什么，大家可以结合图举几个例子就知道了。

处理完了random指针之后，我们就可以将上面那个链表剥离开了，剥离的方法也很简单，那就是创建新链表并进行尾插，这个我们之前有说过，而唯一有点麻烦的依旧是我们要让copy始终指向上面链表的节点，而这个我们在上面也说过了，所以就可以说是没什么难度了，接下来我们直接看本题代码：

/*** Definition for a Node.* struct Node {*     int val;*     struct Node *next;*     struct Node *random;* };*/
typedef struct Node sl;
struct Node* copyRandomList(struct Node* head) {if(head==NULL){return NULL;}//直接创新节点接到原链表的每一个节点后面sl* cur=head;while(cur){sl* copy=(sl*)malloc(sizeof(sl));copy->val=cur->val;copy->next=cur->next;cur->next=copy;cur=copy->next;//挪动指针，不断遍历}cur=head;//重置回头结点sl* copy=cur->next;//接下来处理random指针while(cur){if(cur->random==NULL){copy->random=NULL;}else{copy->random=cur->random->next;}cur=copy->next;if(cur==NULL){break;}copy=cur->next;}//至此处理完毕，我们将复制的节点全部移到新链表中//使用尾插sl* copyhead=NULL;sl* copytail=NULL;cur=head;copy=cur->next;while(cur&©){if(copyhead==NULL){copyhead=copytail=copy;}else{copytail->next=copy;copytail=copytail->next;}cur=copy->next;if(cur==NULL){break;}copy=cur->next;}return copyhead;
}

再给上一版详细注释：

/*** Definition for a Node.* struct Node {*     int val;         // 节点存储的值*     struct Node *next;  // 指向下一个节点的指针（常规链表指针）*     struct Node *random; // 指向链表中任意节点或NULL的随机指针* };*/
// 将结构体Node重命名为sl，简化代码中对结构体的重复书写
typedef struct Node sl;
/*** 函数功能：对带有随机指针的链表进行深拷贝* 深拷贝定义：创建一个全新的链表，新链表中每个节点的值、next指针关系、*            random指针关系与原链表完全一致，但所有指针均指向新链表自身的节点，*            与原链表无任何内存关联（修改新链表不会影响原链表）* 算法核心：采用"原地插入+拆分"策略，避免使用哈希表存储映射关系，优化空间复杂度* 整体步骤：三步法（插入复制节点 → 设置随机指针 → 拆分链表）* 时间复杂度：O(n)（三次遍历链表，n为节点总数）* 空间复杂度：O(1)（仅使用常数个指针变量，不随输入规模增长）* 参数：head - 原链表的头节点（可能为NULL）* 返回值：新复制链表的头节点（若原链表为空则返回NULL）*/
struct Node* copyRandomList(struct Node* head) {// 边界条件处理：如果原链表为空，直接返回NULL（无需复制）if(head == NULL){return NULL;}// 第一步：在原链表每个节点后面插入对应的复制节点// 目的：建立原节点与复制节点的"相邻"映射关系，为后续设置random指针做准备sl* cur = head;  // 定义遍历指针，从原链表头节点开始while(cur != NULL)  // 遍历原链表所有节点{// 1. 创建当前节点的复制节点sl* copy = (sl*)malloc(sizeof(sl));  // 为复制节点分配内存copy->val = cur->val;  // 复制原节点的值（保证值相同）// 2. 将复制节点插入到原节点的后面// 原关系：cur -> cur->next// 插入后：cur -> copy -> cur->nextcopy->next = cur->next;  // 复制节点的next先指向原节点的nextcur->next = copy;        // 原节点的next指向复制节点，完成插入// 3. 移动遍历指针到下一个原节点（跳过刚插入的复制节点）cur = copy->next;  // copy->next是原链表中cur的下一个节点}// 插入完成后，链表结构变为：原1 → 复1 → 原2 → 复2 → ... → 原n → 复n → NULL// 第二步：为所有复制节点设置random指针// 关键原理：若原节点cur的random指向原节点A，则复制节点copy的random必指向A的复制节点A'// 由于第一步已插入复制节点，A'就是A的next（A → A'）cur = head;  // 重置遍历指针到原链表头节点sl* copy = cur->next;  // 复制节点初始化为第一个原节点的复制节点while(cur != NULL)  // 遍历所有原节点{// 处理当前复制节点的random指针if(cur->random == NULL)  // 原节点的random为NULL{copy->random = NULL;  // 复制节点的random也为NULL}else  // 原节点的random指向某个节点A{// A的复制节点是A的next（A' = A->next）copy->random = cur->random->next;}// 移动指针到下一组（原节点+复制节点）cur = copy->next;  // 原节点指针移动到下一个原节点if(cur == NULL)  // 若已遍历完所有原节点，退出循环{break;}copy = cur->next;  // 复制节点指针移动到下一个复制节点}// 至此，所有复制节点的val、next、random均已正确设置// 第三步：将复制节点从原链表中拆分出来，形成独立的新链表// 采用尾插法构建新链表，同时恢复原链表的结构（可选，题目未要求恢复但不影响）sl* copyhead = NULL;  // 新链表的头节点（待确定）sl* copytail = NULL;  // 新链表的尾节点（用于尾插）cur = head;  // 重置遍历指针到原链表头节点copy = cur->next;  // 复制节点指针指向第一个复制节点while(cur != NULL && copy != NULL)  // 遍历所有原节点和复制节点{// 尾插法将复制节点加入新链表if(copyhead == NULL)  // 新链表为空（处理第一个复制节点）{copyhead = copytail = copy;  // 头节点和尾节点都指向第一个复制节点}else  // 新链表已有节点{copytail->next = copy;  // 尾节点的next指向当前复制节点copytail = copytail->next;  // 尾节点后移到当前复制节点}// 移动指针到下一组cur = copy->next;  // 原节点指针后移if(cur == NULL)  // 若已处理完所有节点，退出循环{break;}copy = cur->next;  // 复制节点指针后移}// 拆分完成后，新链表结构：复1 → 复2 → ... → 复n → NULL// 返回新复制链表的头节点return copyhead;
}

结语：在链表的逻辑脉络里，看见算法思维的生长

当我们终于把环形链表的 “追击谜题”、环入口的 “数学密码”，以及随机链表复制的 “映射艺术” 一一拆解透彻时，或许你会和我一样，对 “算法” 二字有了更具体的感知 —— 它从来不是课本里抽象的定义，也不是面试中冰冷的考点，而是用逻辑串联细节、用推导化解困惑的思维工具。这三道链表题，就像三把钥匙，帮我们打开了 “如何用简单方法解决复杂问题” 的大门。

回头再看，这三道题其实围绕着一个核心：如何处理链表中的 “指针关系”。判断环形链表时，我们用快慢指针的 “速度差” 打破线性思维的局限 —— 当快指针像 “追及者” 一样在环内兜转，慢指针像 “探索者” 一样稳步前进，两者的相遇不仅证明了环的存在，更埋下了后续找环入口的伏笔。这个过程里，我们曾纠结 “快指针走 3 步能不能追上”，也曾反复画图确认 “慢指针进环后会不会绕圈”，而正是这些看似 “多余” 的思考，让我们看清了环形结构中 “距离缩减” 的本质规律，也让 “快慢指针走 2 步和 1 步” 的选择从 “习惯” 变成了 “必然”。

找环入口的两种方法，更像是算法思维的 “双面镜”。第一种 “打断环转相交链表” 的思路，教会我们 “转化问题”—— 把陌生的环形问题，变成熟悉的相交链表问题，用已掌握的 “对齐长度、同步遍历” 技巧解决新挑战；第二种 “数学推导” 的方法，则让我们见识到 “规律的力量”—— 当我们把 “头到入口距离”“环入口到相遇点距离”“环长” 这些变量串联成等式，当 “a = k*c - b” 的推导把复杂关系简化为 “头和相遇点同步移动必相遇” 时，突然发现：原来算法的优雅，藏在严谨的数学逻辑里。这些推导过程或许需要反复演算，但每一次确认，都是对 “用数据说话” 的思维习惯的强化。

而随机链表的复制，更像是一场 “精密的工程搭建”。我们没有用哈希表这种 “便捷工具”，而是选择用 “原地插入” 的方式，把复制节点 “贴” 在原节点身后 —— 这个看似朴素的操作，却完美解决了 “原节点与复制节点如何映射” 的核心难题。当我们处理 random 指针时，“原节点 random 的 next 就是复制节点的 random” 这一关联，像一把钥匙打开了锁；当我们用尾插法把复制节点拆分成新链表时，每一步指针移动都需要小心翼翼，生怕破坏了已构建的逻辑。这个过程让我们明白：好的算法不仅要 “能解决问题”，还要 “高效地解决问题”—— 用 O (1) 空间复杂度完成深拷贝，正是 “优化思维” 的最好体现。

很多时候，我们面对算法题会陷入 “畏难情绪”，不是因为知识点不足，而是因为不敢 “沉下去”—— 不敢花时间画图梳理链表结构，不敢反复推导验证数学公式，不敢在调试中一次次修正指针移动的逻辑。就像我在写这篇解析时，曾为了确认 “慢指针进环后是否绕圈”，画了十几张不同环长、不同相遇点的示意图；也曾为了讲清 “为什么能忽略 (m-1)*C”，反复用具体数值代入公式验证。这些看似 “耗时” 的过程，恰恰是算法学习的核心 —— 算法不是 “背答案”，而是 “悟原理”，是在一次次试错与修正中，构建起自己的逻辑体系。

我知道，对于很多初学者来说，链表题或许是编程路上的第一道 “坎”—— 指针的移动、环形的嵌套、随机指针的不确定性，很容易让人陷入 “越想越乱” 的困境。但请相信：每一道让你卡壳的题，都是一次成长的机会。今天你可能需要对着解析一步步看懂逻辑，但明天当你再遇到类似问题时，或许会下意识地拿起笔画图，会尝试用数学公式推导关系，会思考如何用更优的方式减少空间消耗 —— 这些思维习惯的养成，比 “记住一道题的解法” 更有价值。

算法学习就像一场漫长的 “修行”，没有捷径可走，但每一步都算数。今天我们攻克了这三道链表题，明天可能会遇到更复杂的二叉树、动态规划问题，但本质上，解决问题的逻辑是相通的：把复杂问题拆分成简单步骤，用已知规律推导未知结论，用严谨的逻辑验证每一个思路。不要害怕暂时的 “看不懂”，也不用焦虑 “进步太慢”—— 只要你愿意花时间琢磨，愿意在调试中积累经验，每一次思考都会成为你的 “底气”。

最后，我想邀请你做一件事：放下这篇解析，打开编译器，试着自己动手写一遍这三道题的代码。不用急着看答案，哪怕一开始会写错指针移动的顺序，哪怕推导环入口公式时会卡住，哪怕处理随机指针时会出现空指针错误 —— 这些 “错误” 都是学习的一部分。当你终于调试成功，看着程序正确输出结果时，你会感受到一种远超 “看懂解析” 的成就感 —— 那是你亲手构建逻辑、解决问题的力量。

未来的编程路上，还会有无数道算法题等着你，但请记住：每一道题都是一个 “信号”，它在提醒你 —— 算法的本质，是让复杂的世界变得有迹可循。而你要做的，就是带着今天学到的 “拆解思维”“推导习惯”，一步步走下去。相信总有一天，你会回头发现：那些曾经让你头疼的链表题，早已成为你算法思维大厦的基石；而那些反复画图、推导的时光，都变成了照亮你编程之路的光。继续加油吧，每一个在算法路上坚持的人，都在书写属于自己的 “逻辑传奇”。